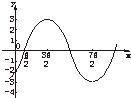
解:(1)如圖
(2)由已知,周期T=
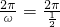
=4π,振幅A=3,初相是-

.
由于y=3sin(x-

)是周期函數,通過觀察圖象可知,所有與x軸垂直并且通過圖象的最值點的直線都是此函數的對稱軸,即令x-

=

+kπ,解得直線方程為x=
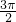
+2kπ,k∈Z;
所有圖象與x軸的交點都是函數的對稱中心,所以對稱中心為點(

+2kπ,0),k∈Z;
x前的系數為正數,所以把x-

視為一個整體,令-

+2kπ≤x-

≤

+2kπ,
解得[-

+4kπ,
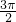
+4kπ],k∈Z為此函數的單調遞增區間.
(3)方法一:“先平移,后伸縮”.
先把y=sinx的圖象上所有的點向右平移

個單位,得到y=sin(x-

)的圖象;再把y=sin(x-

)圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),得到y=sin(x-

)的圖象;最后將y=sin(x-

)的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(x-

)的圖象.
方法二:“先伸縮,后平移”.
先把y=sinx的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),得到y=sin(x)的圖象;再把y=sin(x)圖象上所有的點向右平移

個單位,得到y=sin(x-

)=sin(
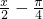
)的圖象;最后將y=sin(x-

)的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(x-

)的圖象.
分析:(1)五點法作圖的五點分別是三個零點與兩個最值點,對此題五點的選取可令相位

x-

為0,

,π,

,2π,求出相應的x的值與y的值;
(2)由三角函數的圖象與性質周期T=
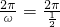
=4π,振幅A=3,初相是-

.結合圖象求出對稱軸方程、對稱中心的坐標、及單調增區間.
(3)方法一:由圖象的變換規則知此函數是由y=sinx的圖象經過先右移四個單位再將再所得圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),然后再將每個點的縱坐標擴大為原來的三倍而等到的.
方法二:先把y=sinx的圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),;再把所得圖象上所有的點向右平移

個單位,最后將y所得到的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(

x-

)的圖象.
點評:考查三角函數的圖象與性質,本題全面地考查了三角函數圖象的畫法,函數圖象的平移,函數圖象的對稱性與圖象的上升與下降趨勢.涉及知識點較多,綜合性較強.

 x-
x- ).
). 解:(1)如圖
解:(1)如圖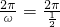 =4π,振幅A=3,初相是-
=4π,振幅A=3,初相是- .
. )是周期函數,通過觀察圖象可知,所有與x軸垂直并且通過圖象的最值點的直線都是此函數的對稱軸,即令x-
)是周期函數,通過觀察圖象可知,所有與x軸垂直并且通過圖象的最值點的直線都是此函數的對稱軸,即令x- =
= +kπ,解得直線方程為x=
+kπ,解得直線方程為x=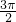 +2kπ,k∈Z;
+2kπ,k∈Z; +2kπ,0),k∈Z;
+2kπ,0),k∈Z; 視為一個整體,令-
視為一個整體,令- +2kπ≤x-
+2kπ≤x- ≤
≤ +2kπ,
+2kπ, +4kπ,
+4kπ,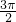 +4kπ],k∈Z為此函數的單調遞增區間.
+4kπ],k∈Z為此函數的單調遞增區間. 個單位,得到y=sin(x-
個單位,得到y=sin(x- )的圖象;再把y=sin(x-
)的圖象;再把y=sin(x- )圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),得到y=sin(x-
)圖象上所有點的橫坐標伸長到原來的2倍(縱坐標不變),得到y=sin(x- )的圖象;最后將y=sin(x-
)的圖象;最后將y=sin(x- )的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(x-
)的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(x- )的圖象.
)的圖象. 個單位,得到y=sin(x-
個單位,得到y=sin(x- )=sin(
)=sin(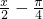 )的圖象;最后將y=sin(x-
)的圖象;最后將y=sin(x- )的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(x-
)的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(x- )的圖象.
)的圖象. x-
x- 為0,
為0, ,π,
,π, ,2π,求出相應的x的值與y的值;
,2π,求出相應的x的值與y的值;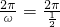 =4π,振幅A=3,初相是-
=4π,振幅A=3,初相是- .結合圖象求出對稱軸方程、對稱中心的坐標、及單調增區間.
.結合圖象求出對稱軸方程、對稱中心的坐標、及單調增區間. 個單位,最后將y所得到的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin(
個單位,最后將y所得到的圖象上所有點的縱坐標伸長到原來的3倍(橫坐標不變),就得到y=3sin( x-
x- )的圖象.
)的圖象.

 閱讀快車系列答案
閱讀快車系列答案 已知函數y=3sin(
已知函數y=3sin(