
 AE,所以異面直線AE與CF所成的角即為∠CFM或其補角,然后在Rt△MEC中,借助正弦或余弦定理解出所求的角.
AE,所以異面直線AE與CF所成的角即為∠CFM或其補角,然后在Rt△MEC中,借助正弦或余弦定理解出所求的角.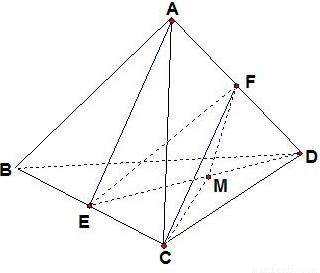 解:如圖所示:設正四面體ABCD的棱長為a,
解:如圖所示:設正四面體ABCD的棱長為a, AE,
AE,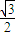 a,
a,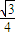 a
a a,EM=
a,EM=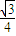 a,
a,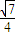 a
a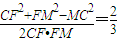
 .
.


 桃李文化快樂暑假武漢出版社系列答案
桃李文化快樂暑假武漢出版社系列答案 優秀生快樂假期每一天全新寒假作業本系列答案
優秀生快樂假期每一天全新寒假作業本系列答案科目:高中數學 來源: 題型:
| AG |
| GD |
| AO |
| OM |
查看答案和解析>>
科目:高中數學 來源: 題型:
| AO |
| OM |
| AO |
| OM |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com