
【題目】對于三次函數![]() ,給出定義:設
,給出定義:設![]() 是函數
是函數![]() 的導數,
的導數,![]() 是
是![]() 的導數,若方程
的導數,若方程![]() 有實數解
有實數解![]() ,則稱點
,則稱點![]() 為函數
為函數![]() 的“拐點”.經過探究發現:任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心,且“拐點”就是對稱中心.設函數
的“拐點”.經過探究發現:任何一個三次函數都有“拐點”;任何一個三次函數都有對稱中心,且“拐點”就是對稱中心.設函數![]() .
.
(1)當![]() 時,求
時,求![]() 的值;
的值;
(2)若不等式![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
 黃岡創優卷系列答案
黃岡創優卷系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為![]() (t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為
(t為參數),若以O為極點,x軸的正半軸為極軸且取相同的單位長度建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求曲線C的直角坐標方程及直線l的普通方程;
(2)將所得曲線C向右平移1個單位長度,再將曲線C上的所有點的橫坐標變為原來的2倍,得到曲線![]() ,求曲線
,求曲線![]() 上的點到直線l的距離的最大值.
上的點到直線l的距離的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】張軍自主創業,在網上經營一家干果店,銷售的干果中有松子、開心果、腰果、核桃,價格依次為120元/千克、80元/千克、70元/千克、40元千克,為增加銷量,張軍對這四種干果進行促銷:一次購買干果的總價達到150元,顧客就少付x(2x∈Z)元.每筆訂單顧客網上支付成功后,張軍會得到支付款的80%.
①若顧客一次購買松子和腰果各1千克,需要支付180元,則x=________;
②在促銷活動中,為保證張軍每筆訂單得到的金額均不低于促銷前總價的七折,則x的最大值為_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校在一次期末數學測試中,為統計學生的考試情況,從學校的2000名學生中隨機抽取50名學生的考試成績,被測學生成績全部介于65分到145分之間(滿分150分),將統計結果按如下方式分成八組:第一組![]() ,第二組
,第二組![]() ,…,第八組
,…,第八組![]() ,如圖是按上述分組方法得到的頻率分布直方圖的一部分.
,如圖是按上述分組方法得到的頻率分布直方圖的一部分.
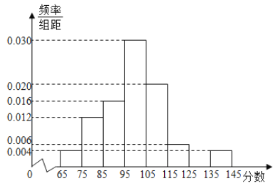
(1)求第七組的頻率;
(2)用樣本數據估計該校的2000名學生這次考試成績的平均分(同一組中的數據用該組區間的中點值代表該組數據平均值);
(3)若從樣本成績屬于第六組和第八組的所有學生中隨機抽取2名,求他們的分差的絕對值小于10分的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).
為參數).
(I)寫出直線![]() 的一般方程與曲線
的一般方程與曲線![]() 的直角坐標方程,并判斷它們的位置關系;
的直角坐標方程,并判斷它們的位置關系;
(II)將曲線![]() 向左平移
向左平移![]() 個單位長度,向上平移
個單位長度,向上平移![]() 個單位長度,得到曲線
個單位長度,得到曲線![]() ,設曲線
,設曲線![]() 經過伸縮變換
經過伸縮變換![]() 得到曲線
得到曲線![]() ,設曲線
,設曲線![]() 上任一點為
上任一點為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】魚卷是泉州十大名小吃之一,不但本地人喜歡,而且深受外來游客的贊賞.小張從事魚卷生產和批發多年,有著不少來自零售商和酒店的客戶當地的習俗是農歷正月不生產魚卷,客戶正月所需要的魚卷都會在上一年農歷十二月底進行一次性采購小張把去年年底采購魚卷的數量x(單位:箱)在![]() 的客戶稱為“熟客”,并把他們去年采購的數量制成下表:
的客戶稱為“熟客”,并把他們去年采購的數量制成下表:
采購數x |
|
|
|
|
|
客戶數 | 10 | 10 | 5 | 20 | 5 |
(1)根據表中的數據作出頻率分布直方圖,并估計采購數在168箱以上(含168箱)的“熟客”人數;
(2)若去年年底“熟客”們采購的魚卷數量占小張去年年底總的銷售量的![]() ,估算小張去年年底總的銷售量(同一組中的數據用該組區間的中點值為代表);
,估算小張去年年底總的銷售量(同一組中的數據用該組區間的中點值為代表);
(3)由于魚卷受到游客們的青睞,小張做了一份市場調查,決定今年年底是否在網上出售魚卷,若不在網上出售魚卷,則按去年的價格出售,每箱利潤為20元,預計銷售量與去年持平;若在網上出售魚卷,則需把每箱售價下調2至5元,且每下調m元(![]() )銷售量可增加1000m箱,求小張今年年底收入Y(單位:元)的最大值.
)銷售量可增加1000m箱,求小張今年年底收入Y(單位:元)的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com