已知直線l:x+2y+1=0,集合A={n|n<6,n∈N*},從A中任取3個不同的元素分別作為圓方程(x-a)2+(y-b)2=r2中的a、b、r,則使圓心(a,b)與原點的連線垂直于直線l的概率等于 .
【答案】
分析:本題是一個等可能事件的概率,試驗發生包含的事件是從5個元素中任取3個分別作為a、b、r,共有A
53種結果,滿足條件的事件是圓心(a,b)與原點的連線垂直于直線l,根據直線垂直的條件寫出a,b之間的關系,列舉出結果數,得到概率.
解答:解:由題意知本題是一個等可能事件的概率,
試驗發生包含的事件是從5個元素中任取3個分別作為圓方程(x-a)
2+(y-b)
2=r
2中的a、b、r,共有A
53=60種結果,
滿足條件的事件是使圓心(a,b)與原點的連線垂直于直線l,即
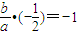
,
∴
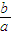
=2,
把一對有序數對分別作為a,b列舉出所有結果,(1,2)(2,4)
確定這兩個數字以后還有一個r的3種不同取法,共有2×3=6種結果,
∴本題要求的概率是
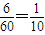
故答案為:
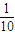 點評:
點評:本題考查等可能事件的概率,考查兩條直線垂直的充要條件,考查利用列舉與組合數相結合的方法得到事件數,本題是一個綜合題目.

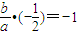 ,
,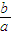 =2,
=2,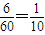
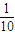


 新編小學單元自測題系列答案
新編小學單元自測題系列答案 字詞句段篇系列答案
字詞句段篇系列答案