
【題目】2016年夏季奧運會將在巴西里約熱內盧舉行,體育頻道為了解某地區關于
奧運會直播的收視情況,隨機抽取了![]() 名觀眾進行調查,其中
名觀眾進行調查,其中![]() 歲以上的觀眾有
歲以上的觀眾有![]() 名,下面是根據
名,下面是根據
調查結果繪制的觀眾準備平均每天收看奧運會直播時間的頻率分布表(時間:分鐘):
分組 |
|
|
|
|
|
|
頻率 |
|
|
|
|
|
|
將每天準備收看奧運會直播的時間不低于![]() 分鐘的觀眾稱為“奧運迷”,已知“奧運迷”中有
分鐘的觀眾稱為“奧運迷”,已知“奧運迷”中有![]() 名
名![]() 歲
歲
以上的觀眾.
(1)根據已知條件完成下面的![]() 列聯表,并據此資料你是否有
列聯表,并據此資料你是否有![]() 以上的把握認為“奧運迷”與年齡
以上的把握認為“奧運迷”與年齡
有關?
非“奧運迷” | “奧運迷” | 合計 | |
| |||
| |||
合計 |
(2)將每天準備收看奧運會直播不低于![]() 分鐘的觀眾稱為“超級奧運迷”,已知“超級奧運迷”中有
分鐘的觀眾稱為“超級奧運迷”,已知“超級奧運迷”中有![]()
名![]() 歲以上的觀眾,若從“超級奧運迷”中任意選取
歲以上的觀眾,若從“超級奧運迷”中任意選取![]() 人,求至少有
人,求至少有![]() 名
名![]() 歲以上的觀眾的概率.
歲以上的觀眾的概率.
附: 
|
|
|
|
|
|
【答案】(1)列聯表見解析,沒有![]() 以上的把握認為“奧運迷”與年齡有關;(2)
以上的把握認為“奧運迷”與年齡有關;(2)![]() .
.
【解析】試題分析:(1)根據已知條件,填寫![]() 聯表,然后根據公式
聯表,然后根據公式 計算得
計算得![]() ,所以沒有
,所以沒有![]() 以上的把握認為“奧運迷”與年齡有關;(2)由頻率分布表可知,“超級奧運迷”有
以上的把握認為“奧運迷”與年齡有關;(2)由頻率分布表可知,“超級奧運迷”有![]() 人,用列舉法列舉出所有的可能性有
人,用列舉法列舉出所有的可能性有![]() 種,其中符合題意的有
種,其中符合題意的有![]() 種,故概率為
種,故概率為![]() .
.
試題解析:
(1)由頻率分布表可知,在軸取的![]() 人中,“奧運迷”有
人中,“奧運迷”有![]() 人,從完成
人,從完成![]() 列聯表如下:
列聯表如下:
非“奧運迷” | “奧運迷” | 合計 | |
|
|
|
|
|
|
|
|
合計 |
|
|
|
![]() .
.
因為![]() ,所以沒有
,所以沒有![]() 以上的把握認為“奧運迷”與年齡有關.
以上的把握認為“奧運迷”與年齡有關.
(2)由頻率分布表可知,“超級奧運迷”有![]() 人,從而所有可能結果所組成的基本事件空間為:
人,從而所有可能結果所組成的基本事件空間為:
![]() 其中
其中![]() 表示男性,
表示男性, ![]() 表示女性,
表示女性, ![]() .
. ![]() 由
由![]() 個基本事件組成,且是等可能的,用
個基本事件組成,且是等可能的,用![]() 表示事件“任意選
表示事件“任意選![]() 人,至少有
人,至少有![]() 名
名![]() 歲以上觀眾”,則
歲以上觀眾”,則![]() ,即事件
,即事件![]() 包含
包含![]() 個基本事件,所以
個基本事件,所以![]() .
.


科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最大值;
上的最大值;
(2)令![]() ,若
,若![]() 在區間
在區間![]() 上為單調遞增函數,求
上為單調遞增函數,求![]() 的取值范圍;
的取值范圍;
(3)當![]() 時,函數
時,函數![]() 的圖象與
的圖象與![]() 軸交于兩點
軸交于兩點![]() 且
且![]() ,又
,又![]() 是
是![]() 的導函數.若正常數
的導函數.若正常數![]() 滿足條件
滿足條件![]() .證明:
.證明:![]() <0.
<0.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正三棱柱ABCA1B1C1中,F,F1分別是AC,A1C1的中點.
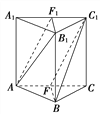
求證:(1)平面AB1F1∥平面C1BF;
(2)平面AB1F1⊥平面ACC1A1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某投資人欲將5百萬元獎金投入甲、乙兩種理財產品,根據銀行預測,甲、乙兩種理財產品的收益與投入獎金![]() 的關系式分別為
的關系式分別為![]() ,其中
,其中![]() 為常數且
為常數且![]() .設對乙種產品投入獎金
.設對乙種產品投入獎金![]() 百萬元,其中
百萬元,其中![]() .
.
(1)當![]() 時,如何進行投資才能使得總收益
時,如何進行投資才能使得總收益![]() 最大;(總收益
最大;(總收益![]() )
)
(2)銀行為了吸儲,考慮到投資人的收益,無論投資人獎金如何分配,要使得總收益不低于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某少數民族的刺繡有著悠久的歷史,下圖![]() 為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含
為她們刺繡最簡單的四個圖案,這些圖案都由小正方形構成,小正方形數越多刺繡越漂亮,現按同樣的規律刺繡(小正方形的擺放規律相同),設第n個圖形包含![]() 個小正方形.
個小正方形.

(1)求出![]() ;
;
(2)利用合情推理的“歸納推理思想”歸納出![]() 與
與![]() 的關系式,
的關系式,
(3)根據你得到的關系式求![]() 的表達式
的表達式
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=ln x-ax(a∈R)(e=2.718 28…是自然對數的底數).
(1)判斷f(x)的單調性;
(2)當f(x)<0在(0,+∞)上恒成立時,求a的取值范圍;
(3)證明:當x∈(0,+∞)時,![]() (1+x)
(1+x) ![]() <e.
<e.
查看答案和解析>>
科目:高中數學 來源: 題型:
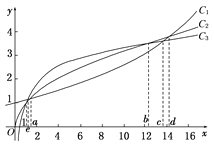
【題目】函數f(x)=1.1x,g(x)=ln x+1,h(x)=x![]() 的圖象如圖所示,試分別指出各曲線對應的函數,并比較三個函數的增長差異(以1,a,b,c,d,e為分界點).
的圖象如圖所示,試分別指出各曲線對應的函數,并比較三個函數的增長差異(以1,a,b,c,d,e為分界點).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com