
【題目】已知函數(shù)![]() .
.
(1)若![]() 是函數(shù)
是函數(shù)![]() 的一個極值點,試討論
的一個極值點,試討論![]() 的單調性;
的單調性;
(2)若![]() 在R上有且僅有一個零點,求
在R上有且僅有一個零點,求![]() 的取值范圍.
的取值范圍.
【答案】(1)當![]() 時,
時,![]() 在
在![]() 上單調遞減;當
上單調遞減;當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;(2)
上單調遞減;(2)![]() .
.
【解析】
(1)根據(jù)極值點處導數(shù)為零,計算出參數(shù)![]() 以及
以及![]() ,再對
,再對![]() 求導,對參數(shù)
求導,對參數(shù)![]() 進行分類討論,從而求得該函數(shù)的單調區(qū)間;
進行分類討論,從而求得該函數(shù)的單調區(qū)間;
(2)分離參數(shù),構造函數(shù),通過討論構造的函數(shù)的單調性求得值域,即可求得參數(shù)![]() 的取值范圍.
的取值范圍.
(1)![]() ,
,
因為![]() 是函數(shù)
是函數(shù)![]() 的一個極值點,
的一個極值點,
則![]() ,所以
,所以![]() ,
,
則![]() ,
,
當![]() ,
,
當![]() 時,
時,![]() 恒成立,
恒成立,
![]() 在
在![]() 上單調遞減,
上單調遞減,
當![]() 時,
時,![]() ,
,
所以![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
綜上所述:
當![]() 時,
時,![]() 在
在![]() 上單調遞減;
上單調遞減;
當![]() 時,
時,![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減.
上單調遞減.
(2)![]() 在
在![]() 上有且僅有一個零點,
上有且僅有一個零點,
即方程![]() 有唯一的解,令
有唯一的解,令![]() ,
,
可得![]() ,
,
由![]() ,
,
得![]() 或
或![]() ,
,
(1)當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,所以
,所以![]() 的取值范圍為
的取值范圍為![]() .
.
(2)當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞增,
上單調遞增,
所以![]() ,即
,即![]() ,
,
故![]() 的取值范圍為
的取值范圍為![]() .
.
(3)當![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調遞減,
上單調遞減,
所以![]() ,即
,即![]() ,
,
即![]() 的取值范圍為
的取值范圍為![]() .
.
所以,當![]() 或
或![]() ,
,
即![]() 或
或![]() 時,
時,![]() 在
在![]() 上有且只有一個零點,
上有且只有一個零點,
故![]() 的取值范圍為
的取值范圍為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】(題文)已知函數(shù)![]() ,其中
,其中![]() 為正實數(shù).
為正實數(shù).
(1)若函數(shù)![]() 在
在![]() 處的切線斜率為2,求
處的切線斜率為2,求![]() 的值;
的值;
(2)求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(3)若函數(shù)![]() 有兩個極值點
有兩個極值點![]() ,求證:
,求證:![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為 (
(![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,以
為極點,以![]() 軸正半軸為極軸,建立極坐標系,直線
軸正半軸為極軸,建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() ,經(jīng)過點
,經(jīng)過點![]() 的直線
的直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,若
兩點,若![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某校為了解學生一周的課外閱讀情況,隨機抽取了100名學生對其進行調查.下面是根據(jù)調查結果繪制的一周學生閱讀時間(單位:分鐘)的頻率分布直方圖,且將一周課外閱讀時間不低于200分鐘的學生稱為“閱讀愛好”,低于200分鐘的學生稱為“非閱讀愛好”.
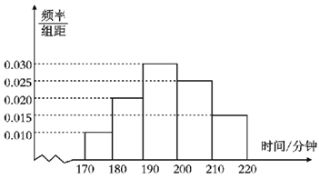
(1)根據(jù)已知條件完成下面![]() 列聯(lián)表,并據(jù)此判斷是否有97.5%的把握認為“閱讀愛好”與性別有關?
列聯(lián)表,并據(jù)此判斷是否有97.5%的把握認為“閱讀愛好”與性別有關?
非閱讀愛好 | 閱讀愛好 | 合計 | |
男女 | 50 | ||
合計 | 14 | ||
男女 |
(2)將頻率視為概率,從該校學生中用隨機抽樣的方法抽取4人,記被抽取的四人中“閱讀愛好”的人數(shù)為![]() ,若每次抽取的結果是相互獨立的,求
,若每次抽取的結果是相互獨立的,求![]() 的分布列和數(shù)學期望
的分布列和數(shù)學期望![]() .
.
附:
| 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com