
定義在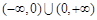 上的函數
上的函數 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列 ,
, 仍是等比數列,則稱
仍是等比數列,則稱 為“保等比數列函數”. 現有定義在
為“保等比數列函數”. 現有定義在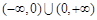 上的如下函數:
上的如下函數:
① ; ②
; ② ; ③
; ③ ; ④
; ④ .
.
則其中是“保等比數列函數”的 的序號為( )
的序號為( )
A.① ② B.③ ④ C.① ③ D.② ④
C
【解析】本題考查等比數列性質及函數計算,正確運算,理解新定義是解題的關鍵
因為由等比數列性質知anan+2=an+12,①f(an)f(an+2)=an2an+22=(an+12) 2=f2(an+1),故正確;
②根據解析式可知f(an)f(an+2)=2an2an+2= 2an+an+2≠22an+1=f2(an+1),故不正確;
③結合已知條件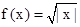 ,則f(an)f(an+2)=
,則f(an)f(an+2)=  f2(an+1),故正確;
f2(an+1),故正確;
④因為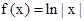 ,那么f(an)f(an+2)=ln|an|ln|an+2|≠ln|an+1|2=f2(an+1),故不正確;
,那么f(an)f(an+2)=ln|an|ln|an+2|≠ln|an+1|2=f2(an+1),故不正確;
故選C。
解決該試題的關鍵是根據新定義,結合等比數列性質anan+2=an+12,一一加以判斷,即可得到結論。


科目:高中數學 來源:2015屆四川成都七中實驗學校高一3月月考數學試卷(解析版) 題型:選擇題
定義在 上的函數
上的函數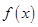 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列 ,
, 仍是等比數列,則稱
仍是等比數列,則稱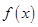 為“保等比數列函數”. 現有定義在
為“保等比數列函數”. 現有定義在 上的如下函數:
上的如下函數:
①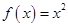 ②
② ③
③ ④
④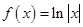
則其中是“保等比數列函數”的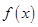 的序號為( )
的序號為( )
A.①② B.③④ C.①③ D.②④
查看答案和解析>>
科目:高中數學 來源:2012年全國普通高等學校招生統一考試理科數學(湖北卷解析版) 題型:選擇題
定義在 上的函數
上的函數 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列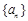 ,
,  仍是等比數列,則稱
仍是等比數列,則稱 為“保等比數列函數”. 現有定義在
為“保等比數列函數”. 現有定義在 上的如下函數:①
上的如下函數:① ; ②
; ② ; ③
; ③ ; ④
; ④ .則其中是“保等比數列函數”的
.則其中是“保等比數列函數”的 的序號為
的序號為
A、① ② B、③ ④ C、① ③ D、② ④
查看答案和解析>>
科目:高中數學 來源:2012年全國普通高等學校招生統一考試文科數學(湖北卷解析版) 題型:選擇題
定義在 上的函數
上的函數 ,如果對于任意給定的等比數列
,如果對于任意給定的等比數列 仍是等比數列,則稱
仍是等比數列,則稱 為“保等比數列函數”。現有定義在
為“保等比數列函數”。現有定義在 上的如下函數:①
上的如下函數:① ;②
;② ;③
;③ ;④
;④ 。則其中是“保等比數列函數”的
。則其中是“保等比數列函數”的 的序號為
的序號為
A、①② B、③④ C、①③ D、②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com