【答案】
分析:(I)把a等于1代入到f(x)中求出f′(x),令f′(x)大于0求出x的范圍即為函數的增區間,令f′(x)小于0求出x的范圍即為函數的減區間;
(II)f(x)小于0時不可能恒成立,所以要使函數在(0,

)上無零點,只需要對x屬于(0,

)時f(x)大于0恒成立,列出不等式解出a大于一個函數,利用導數得到函數的單調性,根據函數的增減性得到這個函數的最大值即可得到a的最小值;
(III)求出g′(x),根據導函數的正負得到函數的單調區間,即可求出g(x)的值域,而當a等于2時不合題意,當a不等于2
時,求出f′(x)=0時x的值,根據x屬于(0,e]列出關于a的不等式得到①,并根據此時的x的值討論導函數的正負得到函數f(x)的單調區間,根據單調區間得到②和③,令②中不等式的坐標為一個函數,求出此函數的導函數,討論導函數的正負得到函數的單調區間,根據函數的增減性得到此函數的最大值,即可解出②恒成立和解出③得到④,聯立①和④即可解出滿足題意a的取值范圍.
解答:解:(I)當a=1時,f(x)=x-1-2lnx,則f'(x)=1-
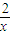
,
由f'(x)>0,得x>2;由f'(x)<0,得0<x<2.
故f(x)的單調減區間為(0,2],單調增區間為[2,+∞);
(II)因為f(x)<0在區間

上恒成立不可能,
故要使函數
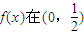
上無零點,
只要對任意的

,f(x)>0恒成立,即對
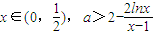
恒成立.
令
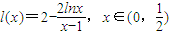
,則
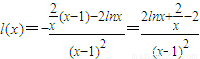
,
再令

,
則
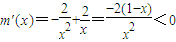
,故m(x)在
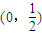
上為減函數,于是
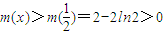
,
從而,l(x)>0,于是l(x)在
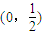
上為增函數,所以

,
故要使
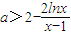
恒成立,只要a∈[2-4ln2,+∞),
綜上,若函數f(x)在
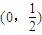
上無零點,則a的最小值為2-4ln2;
(III)g'(x)=e
1-x-xe
1-x=(1-x)e
1-x,
當x∈(0,1)時,g'(x)>0,函數g(x)單調遞增;
當x∈(1,e]時,g'(x)<0,函數g(x)單調遞減.
又因為g(0)=0,g(1)=1,g(e)=e•e
1-e>0,
所以,函數g(x)在(0,e]上的值域為(0,1].
當a=2時,不合題意;當a≠2時,f'(x)=
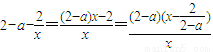
,x∈(0,e]
當x=

時,f'(x)=0.
由題意得,f(x)在(0,e]上不單調,故
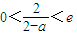
,即

①
此時,當x變化時,f'(x),f(x)的變化情況如下:
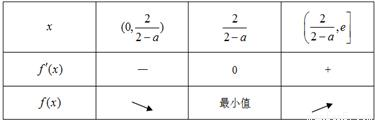
又因為,當x→0時,f(x)→+∞,
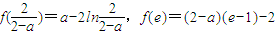
,
所以,對任意給定的x
∈(0,e],在(0,e]上總存在兩個不同的x
i(i=1,2),
使得f(x
i)=g(x
)成立,當且僅當a滿足下列條件:

即
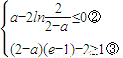
令h(a)=

,
則h
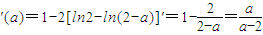
,令h'(a)=0,得a=0或a=2,
故當a∈(-∞,0)時,h'(a)>0,函數h(a)單調遞增;
當
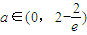
時,h'(a)<0,函數h(a)單調遞減.
所以,對任意
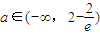
,有h(a)≤h(0)=0,
即②對任意

恒成立.
由③式解得:
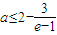
.④
綜合①④可知,當

時,對任意給定的x
∈(0,e],
在(0,e]上總存在兩個不同的x
i(i=1,2),
使f(x
i)=g(x
)成立.
點評:此題考查學生會利用導函數的正負確定函數的單調性,會根據函數的增減性求出閉區間上函數的最值,掌握不等式恒成立時所滿足的條件,是一道壓軸題.

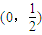 上無零點,求a的最小值;
上無零點,求a的最小值; )上無零點,只需要對x屬于(0,
)上無零點,只需要對x屬于(0, )時f(x)大于0恒成立,列出不等式解出a大于一個函數,利用導數得到函數的單調性,根據函數的增減性得到這個函數的最大值即可得到a的最小值;
)時f(x)大于0恒成立,列出不等式解出a大于一個函數,利用導數得到函數的單調性,根據函數的增減性得到這個函數的最大值即可得到a的最小值;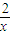 ,
, 上恒成立不可能,
上恒成立不可能,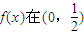 上無零點,
上無零點, ,f(x)>0恒成立,即對
,f(x)>0恒成立,即對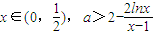 恒成立.
恒成立.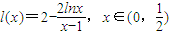 ,則
,則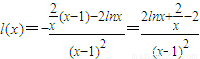 ,
, ,
,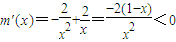 ,故m(x)在
,故m(x)在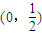 上為減函數,于是
上為減函數,于是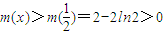 ,
,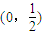 上為增函數,所以
上為增函數,所以 ,
,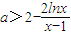 恒成立,只要a∈[2-4ln2,+∞),
恒成立,只要a∈[2-4ln2,+∞),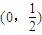 上無零點,則a的最小值為2-4ln2;
上無零點,則a的最小值為2-4ln2;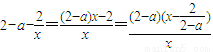 ,x∈(0,e]
,x∈(0,e] 時,f'(x)=0.
時,f'(x)=0.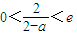 ,即
,即 ①
①
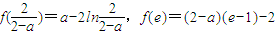 ,
, 即
即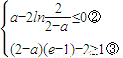
 ,
,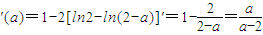 ,令h'(a)=0,得a=0或a=2,
,令h'(a)=0,得a=0或a=2,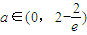 時,h'(a)<0,函數h(a)單調遞減.
時,h'(a)<0,函數h(a)單調遞減.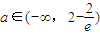 ,有h(a)≤h(0)=0,
,有h(a)≤h(0)=0, 恒成立.
恒成立.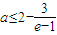 .④
.④ 時,對任意給定的x∈(0,e],
時,對任意給定的x∈(0,e],

 天天向上一本好卷系列答案
天天向上一本好卷系列答案