已知函數f(x)=x2-(2a+1)x+alnx.
(I)當a=2時,求曲線y=f(x)在點(1,f(1))處的切線方程;
(II)求函數f(x)的單調區間;
(III)若對任意a∈(-3,-2)及x∈[1,3]時,恒有ma-f(x)<1成立,求實數m的取值范圍.
解:(I)當a=2時,f(x)=x
2-(2a+1)+alnx=x
2-5x+2lnx
∴f′(x)=2x-5+

∴f′(1)=-1,f(1)=-4,
∴y=f(x)在點(1,f(1))處的切線方程為x+y+3=0
(II)∵f′(x)=2x-(2a+1)+

=
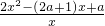
令f′(x)=0,可得
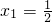
,x
2=a
①當a>

時,由f′(x)>0可得,
f(x)在(0,

),(a,+∞)上單調遞增,
由f′(x)<0可得:
f(x)在(

,a)上單調遞減,
②當a=

時,f′(x)≥0恒成立,
∴f(x)在(0,+∞)上單調遞增;
③當0<a<

時,由f′(x)>0可得
f(x)在(0,a),(

,+∞)上單調遞增,
由f′(x)<0,可得f(x)在(a,

)上單調遞減
④當a≤0時,由f′(x)>0,可得,
f(x)在(

,+∞)上單調遞增,
由f′(x)<0可得f(x)在(0,

)上單調遞減.
(III)由題意可知,對?a∈(-3,-2),x∈[1,3]時,恒有ma-f(x)<1成立
等價于ma-1<f(x)
min,
由(II)知,當a∈(-3,-2)時,f(x)在[1,3]上單調遞增
∴f(x)
min=f(1)=-2a,
∴原題等價于對?a∈(-3,-2)時,ma-1<-2a恒成立,
即m>
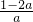
=

-2,在a∈(-3,-2)時,有-

<
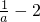
<-

故當m≥-

時,ma-1<-2a恒成立,
∴m≥-

.
分析:(I)當a=2時,f(x)=x
2-(2a+1)+alnx=x
2-5x+2lnx,對f(x)進行求導,求出x=1處的斜率,再根據點斜式求出切線的方程;
(II)對f(x)進行求導,令f′(x)=0,并求出其極值點,從而求出其單調區間;
(III)由題意可知,對?a∈(-3,-2),x∈[1,3]時,恒有ma-f(x)<1成立等價于ma-1<f(x)
min,從而求出m的取值范圍;
點評:此題主要考查利用導數求函數的單調區間,利用導數研究某點的切線方程,關于恒成立的問題,一般都要求函數的最值,此題是一道中檔題.


 =
=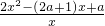
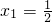 ,x2=a
,x2=a 時,由f′(x)>0可得,
時,由f′(x)>0可得, ),(a,+∞)上單調遞增,
),(a,+∞)上單調遞增, ,a)上單調遞減,
,a)上單調遞減, 時,f′(x)≥0恒成立,
時,f′(x)≥0恒成立, 時,由f′(x)>0可得
時,由f′(x)>0可得 ,+∞)上單調遞增,
,+∞)上單調遞增, )上單調遞減
)上單調遞減 ,+∞)上單調遞增,
,+∞)上單調遞增, )上單調遞減.
)上單調遞減.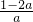 =
= -2,在a∈(-3,-2)時,有-
-2,在a∈(-3,-2)時,有- <
<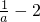 <-
<-
 時,ma-1<-2a恒成立,
時,ma-1<-2a恒成立, .
.

 100分闖關期末沖刺系列答案
100分闖關期末沖刺系列答案 已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<