
 .
.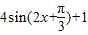 ,由此求得它的對稱中心和單調增區間.
,由此求得它的對稱中心和單調增區間. ,從而得到B的范圍,再根據正弦函數的定義域和值域求得f(B)的最值.
,從而得到B的范圍,再根據正弦函數的定義域和值域求得f(B)的最值. =
=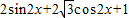 =
=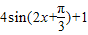 ,…(2分).
,…(2分).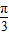 =kπ,k∈z,解得 x=
=kπ,k∈z,解得 x=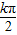 -
-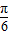 ,k∈z,
,k∈z, …(4分).
…(4分).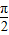 ≤2x+
≤2x+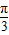 ≤2kπ+
≤2kπ+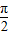 ,k∈Z,求得
,k∈Z,求得 ,
,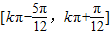 ,k∈Z…(6分).
,k∈Z…(6分).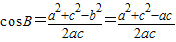
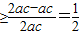 ,∴
,∴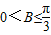 …(8分).
…(8分).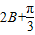 )+1,
)+1,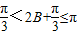 ,
,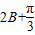 =
=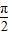 ,即
,即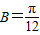 時,f(B)max=5,…(10分).
時,f(B)max=5,…(10分).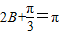 ,即
,即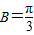 時,f(B)min=1…(12分).
時,f(B)min=1…(12分).

 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源:2012屆山西大學附中高三4月月考理科數學試卷(解析版) 題型:解答題
(本小題共12分)已知函數 的 部 分 圖 象如 圖 所示.
的 部 分 圖 象如 圖 所示.
(I)求 函 數 的
解 析 式;
的
解 析 式;
(II)在△ 中,角
中,角 的
對 邊 分 別 是
的
對 邊 分 別 是 ,若
,若 的
取 值 范 圍.
的
取 值 范 圍.

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com