
【題目】已知函數![]() ,
, ![]() ,其中
,其中![]() 是
是![]() 的導函數.
的導函數.
(Ⅰ)求曲線![]() 在點
在點![]() 處的切線方程;
處的切線方程;
(Ⅱ)若![]() 在
在![]() 上恒成立,求實數
上恒成立,求實數![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】試題分析:(Ⅰ) ![]() ,切線的斜率
,切線的斜率![]() ,所以切線方程為
,所以切線方程為![]() ,即
,即![]() .
.
(Ⅱ)![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() ,構造
,構造![]() 求最小值即可.
求最小值即可.
試題解析:
(Ⅰ)函數![]() 的定義域為
的定義域為![]() ,且
,且![]() ,
,
由導數的幾何意義所求切線的斜率![]() ,
,
所以所求的切線方程為![]() ,即
,即![]() .
.
(Ⅱ)![]() ,
, ![]() ,
,
∴![]() 在
在![]() 上恒成立,
上恒成立,
即![]() ,即
,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() .
.
令![]() ,則
,則 ,
,
令![]() ,
, ![]() ,
,
當![]() 時,
時, ![]() ,∴
,∴![]() 在
在![]() 上單調遞增.
上單調遞增.
∴![]() ,∴
,∴![]() (
(![]() ),
),
∴![]() ,∴
,∴![]() 在
在![]() 上單調遞增,當然在
上單調遞增,當然在![]() 上也單調遞增,
上也單調遞增,
∴![]() ,
,
∴![]() .
.
點晴:本題主要考查導數與切線,導數與極值點、不等式等知識. 解答此類問題,應該首先確定函數的定義域,否則,寫出的單調區(qū)間易出錯. 解決含參數問題及不等式問題注意兩個轉化:(1)利用導數解決含有參數的單調性問題可將問題轉化為不等式恒成立問題,要注意分類討論和數形結合思想的應用.(2)將不等式的證明、方程根的個數的判定轉化為函數的單調性,最值問題處理.


 英語小英雄天天默寫系列答案
英語小英雄天天默寫系列答案 暑假作業(yè)安徽少年兒童出版社系列答案
暑假作業(yè)安徽少年兒童出版社系列答案科目:高中數學 來源: 題型:
【題目】下面幾種推理過程是演繹推理的是 ( )
A. 某校高三(1)班有55人,2班有54人,3班有52人,由此得高三所有班人數超過50人
B. 兩條直線平行,同旁內角互補,如果∠A與∠B是兩條平行直線的同旁內角,則∠A+∠B=180°
C. 由平面三角形的性質,推測空間四邊形的性質
D. 在數列{an}中,a1=1,an=![]() (an-1+
(an-1+![]() )(n≥2),由此歸納出{an}的通項公
)(n≥2),由此歸納出{an}的通項公
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知☉O:x2+y2=1和定點A(2,1),由☉O外一點P(a,b)向☉O引切線PQ,切點為Q,且滿足|PQ|=|PA|.
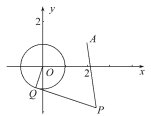
(1)求實數a,b間滿足的等量關系.
(2)求線段PQ長的最小值.
(3)若以P為圓心所作的☉P與☉O有公共點,試求半徑取最小值時☉P的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知長方形![]() ,
, ![]() ,
, ![]() ,以
,以![]() 的中點
的中點![]() 為原點,建立如圖所示的平面直角坐標系
為原點,建立如圖所示的平面直角坐標系![]() .
.
(1)求以![]() 為焦點,且過
為焦點,且過![]() 兩點的橢圓的標準方程;
兩點的橢圓的標準方程;
(2)在(1)的條件下,過點![]() 作直線
作直線![]() 與橢圓交于不同的兩點
與橢圓交于不同的兩點![]() ,設
,設![]() ,點
,點![]() 坐標為
坐標為![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com