
【題目】已知點F1、F2為雙曲線C:x2﹣ ![]() =1的左、右焦點,過F2作垂直于x軸的直線,在x軸上方交雙曲線C于點M,∠MF1F2=30°.
=1的左、右焦點,過F2作垂直于x軸的直線,在x軸上方交雙曲線C于點M,∠MF1F2=30°.
(1)求雙曲線C的方程;
(2)過雙曲線C上任意一點P作該雙曲線兩條漸近線的垂線,垂足分別為P1、P2 , 求 ![]() 的值.
的值.
【答案】
(1)解:設F2,M的坐標分別為 ![]() ,
,
因為點M在雙曲線C上,所以 ![]() ,即
,即 ![]() ,所以
,所以 ![]() ,
,
在Rt△MF2F1中,∠MF1F2=30°, ![]() ,所以
,所以 ![]()
由雙曲線的定義可知: ![]()
故雙曲線C的方程為: ![]()
(2)解:由條件可知:兩條漸近線分別為 ![]()
設雙曲線C上的點Q(x0,y0),設兩漸近線的夾角為θ,
則點Q到兩條漸近線的距離分別為 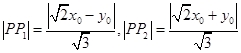 ,
,
因為Q(x0,y0)在雙曲線C: ![]() 上,
上,
所以 ![]() ,又cosθ=﹣
,又cosθ=﹣ ![]() ,
,
所以 ![]() =﹣
=﹣ 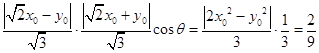
【解析】(1)設F2 , M的坐標分別為 ![]() ,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用雙曲線的定義,即可求雙曲線C的方程;(2)求出兩條漸近線方程,可得點Q到兩條漸近線的距離,設兩漸近線的夾角為θ,可得
,求出|MF2|,Rt△MF2F1中,∠MF1F2=30°,求出|MF1|,利用雙曲線的定義,即可求雙曲線C的方程;(2)求出兩條漸近線方程,可得點Q到兩條漸近線的距離,設兩漸近線的夾角為θ,可得 ![]() ,利用向量的數量積公式,即可求
,利用向量的數量積公式,即可求 ![]() 的值.
的值.


 開心練習課課練與單元檢測系列答案
開心練習課課練與單元檢測系列答案科目:高中數學 來源: 題型:
【題目】下面給出一個問題的算法:
S1 輸入x;
S2 若x≤2,則執行S3;否則,執行S4;
S3 輸出-2x-1;
S4 輸出x2-6x+3.
問題:
(1)這個算法解決的是什么問題?
(2)當輸入的x值為多大時,輸出的數值最小?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為
的棱長為![]() ,
, ![]() 為
為![]() 的中點,
的中點, ![]() 為線段
為線段![]() 上的動點,過點
上的動點,過點![]() ,
, ![]() ,
, ![]() 的平面截該正方體所得的截面為
的平面截該正方體所得的截面為![]() ,則下列命題正確的是__________(寫出所有正確命題的編號).
,則下列命題正確的是__________(寫出所有正確命題的編號).

①當![]() 時,
時, ![]() 為四邊形;②當
為四邊形;②當![]() 時,
時, ![]() 為等腰梯形;
為等腰梯形;
③當![]() 時,
時, ![]() 與
與![]() 的交點
的交點![]() 滿足
滿足![]() ;
;
④當![]() 時,
時, ![]() 為五邊形;
為五邊形;
⑤當![]() 時,
時, ![]() 的面積為
的面積為![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某車間將![]() 名技工平均分成甲、乙兩組加工某種零件,在單位時間內每個技工加工的合格零件數的莖葉圖如圖,已知兩組技工在單位時間內加工的合格零件的平均數都為
名技工平均分成甲、乙兩組加工某種零件,在單位時間內每個技工加工的合格零件數的莖葉圖如圖,已知兩組技工在單位時間內加工的合格零件的平均數都為![]() .
.

(1)求![]() ,
,![]() 的值;
的值;
(2)求甲、乙兩組技工在單位時間內加工的合格零件的方差![]() 和
和![]() ,并由此分析兩組技工的加工水平;
,并由此分析兩組技工的加工水平;
(3)質檢部門從該車間甲、乙兩組技工中各隨機抽取一名,對其加工的零件進行檢測,若兩人加工的合格零件個數之和大于![]() ,則稱該車間“質量合格”,求該車間“質量合格”的概率.
,則稱該車間“質量合格”,求該車間“質量合格”的概率.
附:方差![]() ,其中
,其中![]() 為數據
為數據![]() 的平均數
的平均數
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com