
【題目】已知函數 ![]() ,且f(1)=2,f(2)=3. (I)若f(x)是偶函數,求出f(x)的解析式;
,且f(1)=2,f(2)=3. (I)若f(x)是偶函數,求出f(x)的解析式;
(II)若f(x)是奇函數,求出f(x)的解析式;
(III)在(II)的條件下,證明f(x)在區(qū)間 ![]() 上單調遞減.
上單調遞減.
【答案】解:(I)函數 ![]() ,且f(x)是偶函數,f(1)=2,f(2)=3.則有 f(﹣1)=f(1)=2,
,且f(x)是偶函數,f(1)=2,f(2)=3.則有 f(﹣1)=f(1)=2,
那么:那么: 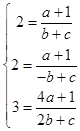 ,解得:a=
,解得:a= ![]() ,b=0,c=
,b=0,c= ![]() .
.
∴f(x)的解析式為f(x)= 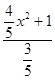 =
= ![]()
(II)f(x)是奇函數,可得f(﹣x)=﹣f(x),則有 f(﹣1)=﹣f(1)=﹣2,
那么: 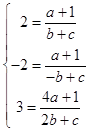 ,解得:a=2,b=
,解得:a=2,b= ![]() ,c=0.
,c=0.
∴f(x)的解析式為f(x)= ![]() .
.
(III)由(II)可得f(x)= ![]() .
.
設 ![]() ,
,
那么:f(x1)﹣f(x2)= ![]() =
= ![]() =
= ![]()
∵ ![]() ,
,
∴ ![]() ,
,
4x1x2﹣2<0.
故:f(x1)﹣f(x2)>0.
所以f(x)在區(qū)間 ![]() 上單調遞減
上單調遞減
【解析】(I)根據f(x)是偶函數,可得f(﹣x)=f(x),那么有 f(﹣1)=f(1)=2,可求a,b,c的值.可得解析式(II)根據f(x)是奇函數,可得f(﹣x)=﹣f(x),那么有 f(﹣1)=﹣f(1)=﹣2,可求a,b,c的值.可得解析式(III)定義法證明其單調性.
【考點精析】本題主要考查了函數單調性的判斷方法的相關知識點,需要掌握單調性的判定法:①設x1,x2是所研究區(qū)間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較才能正確解答此題.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系,將曲線![]() 上的每一個點的橫坐標保持不變,縱坐標縮短為原來的
上的每一個點的橫坐標保持不變,縱坐標縮短為原來的![]() ,得到曲線
,得到曲線![]() ,以坐標原點
,以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸,建立極坐標系,
軸的正半軸為極軸,建立極坐標系, ![]() 的極坐標方程為
的極坐標方程為![]() .
.
(Ⅰ)求曲線![]() 的參數方程;
的參數方程;
(Ⅱ)過原點![]() 且關于
且關于![]() 軸對稱的兩條直線
軸對稱的兩條直線![]() 與
與![]() 分別交曲線
分別交曲線![]() 于
于![]() 、
、![]() 和
和![]() 、
、![]() ,且點
,且點![]() 在第一象限,當四邊形
在第一象限,當四邊形![]() 的周長最大時,求直線
的周長最大時,求直線![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的部分圖象如圖所示.
的部分圖象如圖所示.
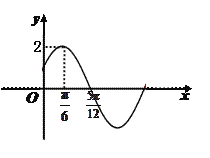
(1) 求函數![]() 的解析式;
的解析式;
(2) 如何由函數![]() 的通過適當圖象的變換得到函數
的通過適當圖象的變換得到函數![]() 的圖象, 寫出變換過程;
的圖象, 寫出變換過程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x-1|+|2x-1|.
(Ⅰ)若對![]() x>0,不等式f(x)≥tx恒成立,求實數t的最大值M;
x>0,不等式f(x)≥tx恒成立,求實數t的最大值M;
(Ⅱ)在(Ⅰ)成立的條件下,正實數a,b滿足a2+b2=2M.證明:a+b≥2ab.
查看答案和解析>>
科目:高中數學 來源: 題型:
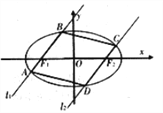
【題目】如圖,過橢圓![]() :
: ![]() 的左右焦點
的左右焦點![]() 分別作直線
分別作直線![]() ,
, ![]() 交橢圓于
交橢圓于![]() 與
與![]() ,且
,且![]() .
.
(1)求證:當直線![]() 的斜率
的斜率![]() 與直線
與直線![]() 的斜率
的斜率![]() 都存在時,
都存在時, ![]() 為定值;
為定值;
(2)求四邊形![]() 面積的最大值.
面積的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知某商品的進貨單價為1元/件,商戶甲往年以單價2元/件銷售該商品時,年銷量為1萬件.今年擬下調銷售單價以提高銷量增加收益.據估算,若今年的實際銷售單價為![]() 元/件(
元/件(![]() ),則新增的年銷量
),則新增的年銷量![]() (萬件).
(萬件).
(1)寫出今年商戶甲的收益![]() (單位:萬元)與
(單位:萬元)與![]() 的函數關系式;
的函數關系式;
(2)商戶甲今年采取降低單價提高銷量的營銷策略,是否能獲得比往年更大的收益(即比往年收益更多)?請說明理由.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com