
【題目】已知動圓Q過定點F(0,﹣1),且與直線y=1相切;橢圓N的對稱軸為坐標軸,中心為坐標原點O,F(xiàn)是其一個焦點,又點(0,2)在橢圓N上.
(1)求動圓圓心Q的軌跡M的方程和橢圓N的方程;
(2)過點(0,﹣4)作直線l交軌跡M于A,B兩點,連結(jié)OA,OB,射線OA,OB交橢圓N于C,D兩點,求△OCD面積的最小值.
(3)附加題:過橢圓N上一動點P作圓x2+(y﹣1)2=1的兩條切線,切點分別為G,H,求 ![]() 的取值范圍.
的取值范圍.
【答案】
(1)解:依題意,由拋物線的定義易得動點Q的軌跡M的標準方程為:x2=﹣4y,
依題意可設橢圓N的標準方程為 ![]() +
+ ![]() =1(a>b>0),
=1(a>b>0),
顯然有c=1,a=2∴b= ![]() ,
,
∴橢圓N的標準方程為: ![]() ;
;
軌跡 ![]()
(2)解: 
所以x1x2+y1y2=0OA⊥OB
設 ![]() ,
,
所以 ![]() ,
,
同理可得: ![]() ,
,
所以 ![]() ,
,
令t=1+k2(t≥1), 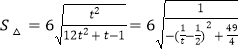 ,
,
所以當 ![]()
(3)解:設∠GPH=2α,圓x2+(y﹣1)2=1的圓心為E,如圖:
當P在橢圓上頂點時PE最小為1,在橢圓下頂點時,|PE|的最大值為3,PE∈[1,3],
PEcosα=PG,sinα= ![]() .
.
∴ 
= 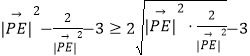 =
= ![]() ,當且僅當|PE|=
,當且僅當|PE|= ![]() 時取等號.
時取等號.
因為|PE|∈[1,3],所以 ![]() .
.
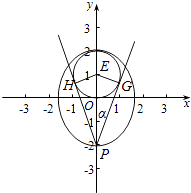
【解析】(1)由拋物線的定義可得動點Q的軌跡M的標準方程,由題意可得c=1,a=2,求得b,進而得到橢圓方程;(2)顯然直線m的斜率存在,不妨設直線m的直線方程為:y=kx﹣4,分別代入拋物線方程和橢圓方程,運用韋達定理和弦長公式,以及點到直線的距離公式,求得三角形的面積,再由不等式的性質(zhì),即可得到所求最小值.(3)設∠EPF=2α,求出 ![]() 表達式,利用
表達式,利用 ![]() 的范圍,求解表達式的范圍即可.
的范圍,求解表達式的范圍即可.
【考點精析】本題主要考查了橢圓的標準方程的相關(guān)知識點,需要掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() 才能正確解答此題.
才能正確解答此題.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優(yōu)練測系列答案
世紀百通優(yōu)練測系列答案 百分學生作業(yè)本題練王系列答案
百分學生作業(yè)本題練王系列答案科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,一個圓柱形乒乓球筒,高為![]() 厘米,底面半徑為
厘米,底面半徑為![]() 厘米.球筒的上底和下底分別粘有一個乒乓球,乒乓球與球筒底面及側(cè)面均相切(球筒和乒乓球厚度忽略不計).一個平面與兩乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個橢圓,則該橢圓的離心率為( )
厘米.球筒的上底和下底分別粘有一個乒乓球,乒乓球與球筒底面及側(cè)面均相切(球筒和乒乓球厚度忽略不計).一個平面與兩乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個橢圓,則該橢圓的離心率為( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知{an}是等差數(shù)列,滿足a1=3,a4=12,數(shù)列{bn}滿足b1=4,b4=20,且{bn﹣an}為等比數(shù)列.
(1)求數(shù)列{an}和{bn}的通項公式;
(2)求數(shù)列{bn}的前n項和.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】定義在![]() 上的函數(shù)
上的函數(shù)![]() ,若
,若![]() ,有
,有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為定義在
為定義在![]() 上的非嚴格單增函數(shù);若
上的非嚴格單增函數(shù);若![]() ,有
,有![]() ,則稱函數(shù)
,則稱函數(shù)![]() 為定義在
為定義在![]() 上的非嚴格單減函數(shù).
上的非嚴格單減函數(shù). ![]() .
.
(1)若函數(shù)![]() 為定義在
為定義在![]() 上的非嚴格單增函數(shù),求實數(shù)
上的非嚴格單增函數(shù),求實數(shù)![]() 的取值范圍.
的取值范圍.
(2)若函數(shù)![]() 為定義在
為定義在![]() 上的非嚴格單減函數(shù),試解不等式
上的非嚴格單減函數(shù),試解不等式![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓C: ![]() +
+ ![]() =1(a>b>0),直線y=x+
=1(a>b>0),直線y=x+ ![]() 與以原點為圓心,以橢圓C的短半軸為半徑的圓相切,F(xiàn)1 , F2為其左右焦點,P為橢圓C上的任意一點,△F1PF2的重心為G,內(nèi)心為I,且IG∥F1F2 .
與以原點為圓心,以橢圓C的短半軸為半徑的圓相切,F(xiàn)1 , F2為其左右焦點,P為橢圓C上的任意一點,△F1PF2的重心為G,內(nèi)心為I,且IG∥F1F2 .
(1)求橢圓C的方程;
(2)已知A為橢圓C上的左頂點,直線∫過右焦點F2與橢圓C交于M,N兩點,若AM,AN的斜率k1 , k2滿足k1+
k2=﹣ ![]() ,求直線MN的方程.
,求直線MN的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某特色餐館開通了美團外賣服務,在一周內(nèi)的某特色菜外賣份數(shù)![]() (份)與收入
(份)與收入![]() (元)之間有如下的對應數(shù)據(jù):
(元)之間有如下的對應數(shù)據(jù):
外賣份數(shù) | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |

(1)畫出散點圖;
(2)求回歸直線方程;
(3)據(jù)此估計外賣份數(shù)為12份時,收入為多少元.
注:①參考公式:線性回歸方程系數(shù)公式 ,
, ![]() ;
;
②參考數(shù)據(jù): ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】所謂正三棱錐,指的是底面為正三角形,頂點在底面上的射影為底面三角形中心的三棱錐,在正三棱錐S﹣ABC中,M是SC的中點,且AM⊥SB,底面邊長AB=2 ![]() ,則正三棱錐S﹣ABC的體積為 , 其外接球的表面積為 .
,則正三棱錐S﹣ABC的體積為 , 其外接球的表面積為 .
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設圓![]() 滿足:(1)截
滿足:(1)截![]() 軸所得弦長為2;(2)被
軸所得弦長為2;(2)被![]() 軸分成兩段圓弧,其弧長的比為
軸分成兩段圓弧,其弧長的比為![]() .在滿足條件(1)、(2)的所有圓中,圓心到直線
.在滿足條件(1)、(2)的所有圓中,圓心到直線![]() 的距離最小的圓的方程為__________.
的距離最小的圓的方程為__________.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知幾何體A﹣BCED的三視圖如圖所示,其中俯視圖和側(cè)視圖都是腰長為4的等腰直角三角形,正視圖為直角梯形. 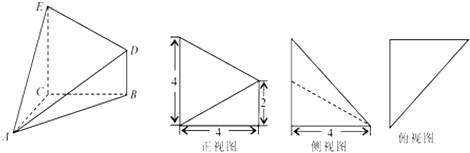
(1)求此幾何體的體積V的大小;
(2)求異面直線DE與AB所成角的余弦值;
(3)求二面角A﹣ED﹣B的正弦值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com