【答案】
分析:(Ⅰ)根據(jù)曲線C:x
2-y
2=1上的點(diǎn)P到點(diǎn)A
n(0,a
n)的距離的最小值為d
n,設(shè)點(diǎn)P(x,y),利用兩點(diǎn)間的距離公式,再采用配方法可得,再根據(jù)

,可得

,從而可得

,從而數(shù)列

是首項(xiàng)

,公差為2的等差數(shù)列,進(jìn)而可求數(shù)列{a
n}的通項(xiàng)公式;
(Ⅱ)先判斷a
2n+2a
2n-1<a
2n+1a
2n,從而有

,所以

,疊加可得結(jié)論;
(Ⅲ)先證明

,從而可得

,進(jìn)而可知存在常數(shù)

,對?n∈N
*,都有不等式:

成立.
解答:(Ⅰ)解:設(shè)點(diǎn)P(x,y),則x
2-y
2=1,所以

,
因?yàn)閥∈R,所以當(dāng)

時(shí),|PA
n|取得最小值d
n,且

,
又

,所以

,即

將

代入

得

兩邊平方得

,又a
=0,

故數(shù)列

是首項(xiàng)

,公差為2的等差數(shù)列,所以

,
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/20131024185850280565429/SYS201310241858502805654020_DA/25.png">>0,所以

.…(6分)
(Ⅱ)證明:因?yàn)椋?n+2)(2n-1)-2n(2n+1)=-2<0,
所以(2n+2)(2n-1)<2n(2n+1)
所以

,所以a
2n+2a
2n-1<a
2n+1a
2n所以

,所以

以上n個(gè)不等式相加得

.…(10分)
(Ⅲ)解:因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/20131024185850280565429/SYS201310241858502805654020_DA/31.png">,當(dāng)k≥2時(shí),

,
因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/20131024185850280565429/SYS201310241858502805654020_DA/33.png">,
所以

所以

,

所以

.
故存在常數(shù)

,對?n∈N
*,都有不等式:

成立.…(14分)
點(diǎn)評:本題考查數(shù)列的通項(xiàng),考查數(shù)列與不等式的綜合,考查放縮法的運(yùn)用,解題的關(guān)鍵是根據(jù)目標(biāo),適當(dāng)放縮,難度較大.

 ,n∈N*.
,n∈N*. ;
; 成立?請說明理由.
成立?請說明理由. ,可得
,可得 ,從而可得
,從而可得 ,從而數(shù)列
,從而數(shù)列 是首項(xiàng)
是首項(xiàng) ,公差為2的等差數(shù)列,進(jìn)而可求數(shù)列{an}的通項(xiàng)公式;
,公差為2的等差數(shù)列,進(jìn)而可求數(shù)列{an}的通項(xiàng)公式; ,所以
,所以 ,疊加可得結(jié)論;
,疊加可得結(jié)論; ,從而可得
,從而可得 ,進(jìn)而可知存在常數(shù)
,進(jìn)而可知存在常數(shù) ,對?n∈N*,都有不等式:
,對?n∈N*,都有不等式: 成立.
成立. ,
, 時(shí),|PAn|取得最小值dn,且
時(shí),|PAn|取得最小值dn,且 ,
, ,所以
,所以 ,即
,即
 代入
代入 得
得
 ,又a=0,
,又a=0,
 是首項(xiàng)
是首項(xiàng) ,公差為2的等差數(shù)列,所以
,公差為2的等差數(shù)列,所以 ,
, .…(6分)
.…(6分) ,所以a2n+2a2n-1<a2n+1a2n
,所以a2n+2a2n-1<a2n+1a2n ,所以
,所以
 .…(10分)
.…(10分) ,
,
 ,
,
 .
. ,對?n∈N*,都有不等式:
,對?n∈N*,都有不等式: 成立.…(14分)
成立.…(14分)


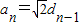 ,n∈N*.
,n∈N*.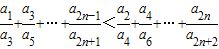 ;
;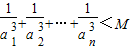 成立?請說明理由.
成立?請說明理由.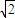 dn-1,n∈N*.
dn-1,n∈N*.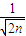 =0的距離為tn,證明:對?n∈N*,都有不等式:t1+t2+…+tn<
=0的距離為tn,證明:對?n∈N*,都有不等式:t1+t2+…+tn< 成立.
成立.