
【題目】“活水圍網”養魚技術具有養殖密度高、經濟效益好的特點.研究表明:“活水圍網”養魚時,某種魚在一定的條件下,每尾魚的平均生長速度v(單位:千克/年)是養殖密度x (單位:尾/立方米)的函數.當x不超過4尾/立方米時,v的值為2千克/年;當4<x≤20時,v是x的一次函數,當x達到20尾/立方米時,因缺氧等原因,v的值為0千克/年.
(1)當0<x≤20時,求v關于x的函數表達式;
(2)當養殖密度x為多大時,魚的年生長量(單位:千克/立方米)可以達到最大?并求出最大值.
【答案】
(1)解:由題意得當0<x≤4時,v=2;
當4<x≤20時,設v=ax+b,
由已知得: ![]() ,解得:
,解得: 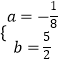 ,
,
所以v=﹣ ![]() x+
x+ ![]() ,
,
故函數v= 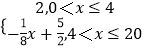
(2)解:設年生長量為f(x)千克/立方米,
依題意并由(1)可得f(x)= 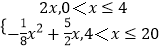
當0<x≤4時,f(x)為增函數,故f(x)max=f(4)=4×2=8;
當4<x≤20時,f(x)=﹣ ![]() x2+
x2+ ![]() x=﹣
x=﹣ ![]() (x2﹣20x)=﹣
(x2﹣20x)=﹣ ![]() (x﹣10)2+
(x﹣10)2+ ![]() ,
,
f(x)max=f(10)=12.5.
所以當0<x≤20時,f(x)的最大值為12.5.
即當養殖密度為10尾/立方米時,魚的年生長量可以達到最大,最大值為12.5千克/立方米
【解析】(1)當4<x≤20時,設v=ax+b,根據待定系數法求出a,b的值,從而求出函數的解析式即可;(2)根據f(x)的表達式,結合二次函數的性質求出f(x)的最大值即可.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和Sn=4n,數列{bn}滿足b1=-3,
bn+1=bn+(2n-3)(n∈N*).
(1)求數列{an}的通項公式;
(2)求數列{bn}的通項公式;
(3)若cn=![]() ,求數列{cn}的前n項和Tn.
,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知y=f(x)是定義在R上的偶函數,當x≥0時,f(x)=x2﹣2x.
(1)求f(x)的解析式;
(2)作出函數f(x)的圖象,并指出其單調區間.(不需要嚴格證明)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知全集U=R,集合A={x|4≤2x<128},B={x|1<x≤6},M={x|a﹣3<x<a+3}.
(1)求A∩UB;
(2)若M∪UB=R,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 和
和![]() 中,已知
中,已知![]() ,且
,且![]() ,
, ![]() ,若數列
,若數列![]() 為等比數列.
為等比數列.
(Ⅰ)求![]() 及數列
及數列![]() 的通項公式;
的通項公式;
(Ⅱ)令![]() ,是否存在正整數
,是否存在正整數![]() ,
, ![]() (
(![]() ),使
),使![]() ,
, ![]() ,
, ![]() 成等差數列?若存在,求出
成等差數列?若存在,求出![]() ,
, ![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知平面直角坐標系![]() ,以
,以![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系,
軸的非負半軸為極軸建立極坐標系, ![]() 點的極坐標為
點的極坐標為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)寫出點![]() 的直角坐標及曲線
的直角坐標及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若![]() 為曲線
為曲線![]() 上的動點,求
上的動點,求![]() 的中點
的中點![]() 到直線
到直線![]() :
: ![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com