在等差數列{an}中,若a1+a7+a8+a12=12,則此數列的前13項的和為________.
39
分析:將a
1+a
7+a
8+a
12用a
1和d表示,再將s
13用a
1和d表示,從中尋找關系即可解決此數列的前13項的和問題.
解答:設等差數列{a
n}的公差為d,
∵a
1+a
7+a
8+a
12=a
1+a
1+6d+a
1+7d+a
1+11d=4a
1+24d=12,
∴a
1+6d=3,
∴s
13=13a
1+
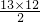
d=13(a
1+6d)=39,
故答案為:39.
點評:此題考查學生掌握等差數列的性質,靈活運用等差數列的通項公式及前n項和的公式化簡求值,是一道基礎題.
