
【題目】如圖,在平面直角坐標(biāo)系![]() 中,已知以
中,已知以![]() 為圓心的圓
為圓心的圓![]() 及其上一點
及其上一點![]() .
.
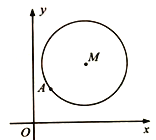
(1)設(shè)圓![]() 與
與![]() 軸相切,與圓
軸相切,與圓![]() 外切,且圓心
外切,且圓心![]() 在直線
在直線![]() 上,求圓
上,求圓![]() 的標(biāo)準(zhǔn)方程;
的標(biāo)準(zhǔn)方程;
(2)設(shè)平行于![]() 的直線
的直線![]() 與圓
與圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的方程.
的方程.
【答案】(1) ![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() .
.
【解析】試題分析:(1)將圓![]() 化為標(biāo)準(zhǔn)方程,求得圓心和半徑,直線
化為標(biāo)準(zhǔn)方程,求得圓心和半徑,直線![]() 的斜率和切線的斜率,由點斜式方程即可得到所求切線的方程;(2)由題意得
的斜率和切線的斜率,由點斜式方程即可得到所求切線的方程;(2)由題意得![]() ,設(shè)
,設(shè)![]() ,則圓心
,則圓心![]() 到直線
到直線![]() 的距離
的距離![]() ,由此能求出直線
,由此能求出直線![]() 的方程.
的方程.
試題解析:圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() 所以圓心
所以圓心![]() ,半徑為
,半徑為![]() .
.
(1)由圓心在直線![]() 上,可設(shè)
上,可設(shè)![]() ,因為
,因為![]() 與
與![]() 軸相切,與圓
軸相切,與圓![]() 外切,所以
外切,所以![]() ,于是圓
,于是圓![]() 的半徑為
的半徑為![]() ,從而
,從而![]() ,解得
,解得![]() ,因此圓
,因此圓![]() 的標(biāo)準(zhǔn)方程為
的標(biāo)準(zhǔn)方程為![]() .
.
(2)因為直線![]() ,所以直線
,所以直線![]() 的斜率為
的斜率為![]() ,設(shè)直線
,設(shè)直線![]() 的方程為
的方程為![]() ,即
,即![]() ,則圓心
,則圓心![]() 到直線
到直線![]() 的距離
的距離![]() ,
,
因為![]() ,而
,而![]() ,所以
,所以![]() ,解得
,解得![]() 或
或![]() ,故直線
,故直線![]() 的方程為
的方程為![]() 或
或![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù) ![]() .
.
(I) 討論函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(II)當(dāng)![]() 時,若函數(shù)
時,若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值為3,求
上的最大值為3,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某醫(yī)藥研究所開發(fā)一種新藥,如果成年人按規(guī)定的劑量服用,據(jù)監(jiān)測,服藥后每毫升血液中的含藥量y(微克)與時間t(小時)之間近似滿足如圖所示的曲線.據(jù)進(jìn)一步測定,每毫升血液中含藥量不少于0.25微克時,治療疾病有效,則服藥一次治療該疾病有效的時間為( ) 
A.4小時
B.![]()
C.![]()
D.5小時
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知定義在(﹣1,1)上的函數(shù)f(x)滿足:對任意x,y∈(﹣1,1)都有f(x)+f(y)=f(x+y).
(Ⅰ)求證:函數(shù)f(x)是奇函數(shù);
(Ⅱ)如果當(dāng)x∈(﹣1,0]時,有f(x)<0,試判斷f(x)在(﹣1,1)上的單調(diào)性,并用定義證明你的判斷;
(Ⅲ)在(Ⅱ)的條件下,若a﹣8x+1>0對滿足不等式f(x﹣ ![]() )+f(
)+f( ![]() ﹣2x)<0的任意x恒成立,求a的取值范圍.
﹣2x)<0的任意x恒成立,求a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)數(shù)f(log2x)的定義域是(2,4),則函數(shù) ![]() 的定義域是( )
的定義域是( )
A.(2,4)
B.(2,8)
C.(8,32)
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某公司生產(chǎn)一種產(chǎn)品,第一年投入資金1000萬元,出售產(chǎn)品收入40萬元,預(yù)計以后每年的投入資金是上一年的一半,出售產(chǎn)品所得收入比上一年多80萬元,同時,當(dāng)預(yù)計投入的資金低于20萬元時,就按20萬元投入,且當(dāng)年出售產(chǎn)品收入與上一年相等.
(1)求第![]() 年的預(yù)計投入資金與出售產(chǎn)品的收入;
年的預(yù)計投入資金與出售產(chǎn)品的收入;
(2)預(yù)計從哪一年起該公司開始盈利?(注:盈利是指總收入大于總投入)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 的參數(shù)方程為
的參數(shù)方程為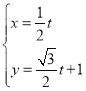 (
(![]() 為參數(shù)),曲線
為參數(shù)),曲線![]() 的普通方程為
的普通方程為![]() ,以坐標(biāo)原點為極點,
,以坐標(biāo)原點為極點,![]() 軸的正半軸為極軸建立極坐標(biāo)系.
軸的正半軸為極軸建立極坐標(biāo)系.
(I)求直線![]() 的極坐標(biāo)方程與曲線
的極坐標(biāo)方程與曲線![]() 的參數(shù)方程;
的參數(shù)方程;
(II)設(shè)點D在曲線![]() 上,且曲線
上,且曲線![]() 在點D處的切線與直線
在點D處的切線與直線![]() 垂直,試確定點D的坐標(biāo).
垂直,試確定點D的坐標(biāo).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]() .
.
(Ⅰ)求函數(shù)f(x)的定義域;
(Ⅱ)判定f(x)的奇偶性并證明;
(Ⅲ)用函數(shù)單調(diào)性定義證明:f(x)在(1,+∞)上是增函數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】對于任意實數(shù)x,不等式ax2+2ax﹣(a+2)<0恒成立,則實數(shù)a的取值范圍是( )
A.﹣1≤a≤0
B.﹣1≤a<0
C.﹣1<a≤0
D.﹣1<a<0
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com