
【題目】若存在實數k,b,使得函數![]() 和
和![]() 對其定義域上的任意實數x同時滿足:
對其定義域上的任意實數x同時滿足:![]() 且
且![]() ,則稱直線:
,則稱直線:![]() 為函數
為函數![]() 和
和![]() 的“隔離直線”.已知
的“隔離直線”.已知![]() ,
,![]() (其中e為自然對數的底數).試問:
(其中e為自然對數的底數).試問:
(1)函數![]() 和
和![]() 的圖象是否存在公共點,若存在,求出交點坐標,若不存在,說明理由;
的圖象是否存在公共點,若存在,求出交點坐標,若不存在,說明理由;
(2)函數![]() 和
和![]() 是否存在“隔離直線”?若存在,求出此“隔離直線”的方程;若不存在,請說明理由.
是否存在“隔離直線”?若存在,求出此“隔離直線”的方程;若不存在,請說明理由.
【答案】(1)存在,交點坐標為![]() ;(2)存在,
;(2)存在,![]()
【解析】
(1)構造函數![]() ,求導得到函數的單調區間,得到函數在
,求導得到函數的單調區間,得到函數在![]() 處取得最小值為0,得到答案.
處取得最小值為0,得到答案.
(2)設直線![]() ,根據
,根據![]() 得到
得到![]() ,再證明
,再證明![]() 恒成立,令
恒成立,令![]() ,求導得到單調區間,計算最值得到證明.
,求導得到單調區間,計算最值得到證明.
(1)∵![]() ,
,
∴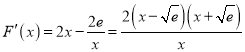 ,令
,令![]() ,得
,得![]() ,
,
當![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
故當![]() 時,
時,![]() 取到最小值,最小值是0,
取到最小值,最小值是0,
從而函數![]() 和
和![]() 的圖象在
的圖象在![]() 處有公共點,交點坐標為
處有公共點,交點坐標為![]() .
.
(2)由(1)可知,函數![]() 和
和![]() 的圖象在
的圖象在![]() 處有公共點,
處有公共點,
因此存在![]() 和
和![]() 的隔離直線,那么該直線過這個公共點,
的隔離直線,那么該直線過這個公共點,
設隔離直線的斜率為k,則隔離直線方程為![]() ,
,
即![]() ,
,
由![]() ,可得
,可得![]() 在
在![]() 上恒成立,
上恒成立,
則![]() ,只有
,只有![]() ,
,
此時直線方程為:![]() ,下面證明
,下面證明![]() 恒成立,
恒成立,
令![]() ,
,
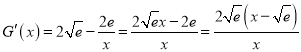 ,當
,當![]() 時,
時,![]() ,
,
當![]() 時
時![]() ,函數單調遞減;
,函數單調遞減;![]() 時,
時,![]() ,函數單調遞增,
,函數單調遞增,
則當![]() 時,
時,![]() 取到最小值是0,
取到最小值是0,
所以![]() ,則
,則![]() 當
當![]() 時恒成立.
時恒成立.
∴函數![]() 和
和![]() 存在唯一的隔離直線
存在唯一的隔離直線![]() .
.


科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的右焦點為
的右焦點為![]() ,過點
,過點![]() 且垂直于
且垂直于![]() 軸的弦長為3,直線
軸的弦長為3,直線![]() 與圓
與圓![]() 相切,且與橢圓
相切,且與橢圓![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() 為橢圓的右頂點.
為橢圓的右頂點.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)用![]() ,
,![]() 分別表示
分別表示![]() 和
和![]() 的面積,求
的面積,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天干地支紀年法源于中國,中國自古便有十天干與十二地支,十天干即甲、乙、丙、丁、戊、己、庚、辛、壬、癸;十二地支即子、丑、寅、卯、辰、已、午、未、申、酉、戌、亥天干地支紀年法是按順序以一個天干和一個地支相配,排列起來,天干在前,地支在后,天干由“甲”起,地支由“子”起,例如,第一年為“甲子”,第二年為“乙丑”,第三年為“丙寅”,…,以此類推,排列到“癸酉”后,天于回到“甲”重新開始,即“甲戌”,“乙亥”,然后地支回到“子”重新開始,即“丙子”,以此類推已知1949年為“己丑”年,那么到中華人民共和國成立70年時為( )
A.丙酉年B.戊申年C.己申年D.己亥年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某次知識競賽規則如下:在主辦方預設的7個問題中,選手若能連續正確回答出兩個問題,即停止答題,晉級下一輪.假設某選手正確回答每個問題的概率都是0.7,且每個問題的回答結果相互獨立,則該選手恰好回答了5個問題就晉級下一輪的概率等于( )
A.0.07497B.0.92503C.0.1323D.0.6174
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,△PAD為等邊三角形,AB=AD![]() CD=2,∠BAD=∠ADC=90°,∠PDC=60°,E為BC的中點.
CD=2,∠BAD=∠ADC=90°,∠PDC=60°,E為BC的中點.
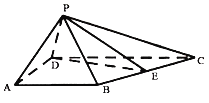
(1)證明:AD⊥PE.
(2)求直線PA與平面PDE所成角的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在矩形ABCD中,![]() ,
,![]() ,沿矩形對角線BD將
,沿矩形對角線BD將![]() 折起形成四面體ABCD,在這個過程中,現在下面四個結論:①在四面體ABCD中,當
折起形成四面體ABCD,在這個過程中,現在下面四個結論:①在四面體ABCD中,當![]() 時,
時,![]() ;②四面體ABCD的體積的最大值為
;②四面體ABCD的體積的最大值為![]() ;③在四面體ABCD中,BC與平面ABD所成角可能為
;③在四面體ABCD中,BC與平面ABD所成角可能為![]() ;④四面體ABCD的外接球的體積為定值.其中所有正確結論的編號為( )
;④四面體ABCD的外接球的體積為定值.其中所有正確結論的編號為( )
A.①④B.①②C.①②④D.②③④
查看答案和解析>>
科目:高中數學 來源: 題型:
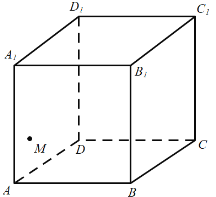
【題目】如圖,點![]() 是正方體
是正方體![]() 中的側面
中的側面![]() 上的一個動點,則下列結論正確的是( )
上的一個動點,則下列結論正確的是( )
A.點![]() 存在無數個位置滿足
存在無數個位置滿足![]()
B.若正方體的棱長為1,三棱錐![]() 的體積最大值為
的體積最大值為![]()
C.在線段![]() 上存在點
上存在點![]() ,使異面直線
,使異面直線![]() 與
與![]() 所成的角是
所成的角是![]()
D.點![]() 存在無數個位置滿足到直線
存在無數個位置滿足到直線![]() 和直線
和直線![]() 的距離相等.
的距離相等.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com