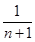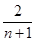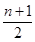已知
Sn是數列{
an}的前
n項和,且
an=
Sn-1+2(
n≥2),
a1=2.
(1)求數列{
an}的通項公式.
(2)設
bn=
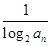
,
Tn=
bn+1+
bn+2+…+
b2n,是否存在最大的正整數
k,使得
對于任意的正整數
n,有
Tn>
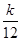
恒成立?若存在,求出
k的值;若不存在,說明理由.
(1)由已知
an=
Sn-1+2, ①
得
an+1=
Sn+2. ②
②-①,得
an+1-
an=
Sn-
Sn-1(
n≥2),
∴
an+1=2
an(
n≥2).
又
a1=2,∴
a2=
a1+2=4=2
a1,
∴
an+1=2
an(
n=1,2,3,…),
∴數列{
an}是一個以2為首項,2為公比的等比數列,
∴
an=2·2
n-1=2
n,
n∈N
*.
(2)
bn=
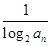
=
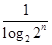
=
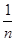
,∴
Tn=
bn+1+
bn+2+…+
b2n=
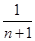
+
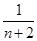
+…+
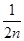
,
Tn+1=
bn+2+
bn+3+…+
b2(n+1)=
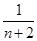
+

+…+
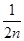
+
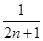
+

.
∴
Tn+1-
Tn=
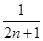
+

-
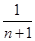
=

=

.
∵
n是正整數,∴
Tn+1-
Tn>0,即
Tn+1>
Tn.
∴數列{
Tn}是一個單調遞增數列.又
T1=
b2=
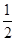
,∴
Tn≥
T1=
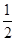
,
要使
Tn>
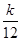
恒成立,則
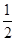
>
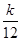
,即
k<6.又
k是正整數,故存在最大正整數
k=5使
Tn>
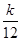
恒成立.
練習冊系列答案
相關習題
科目:高中數學
來源:不詳
題型:解答題
已知首項為
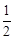
的等比數列{a
n}是遞減數列,其前n項和為S
n,且S
1+a
1,S
2+a
2,S
3+a
3成等差數列.
(Ⅰ)求數列{a
n}的通項公式;
(Ⅱ)若
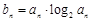
,數列{b
n}的前n項和T
n,求滿足不等式
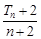
≥
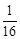
的最大n值.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
在等差數列{
an}中,
a8=
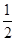 a11
a11+6,則數列{
an}前9項的和
S9等于( ).
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
設等差數列{
an}的前
n項和為
Sn,若
a1=-15,
a3+
a5=-18,則當
Sn取最小值時
n等于( ).
查看答案和解析>>
科目:高中數學
來源:不詳
題型:解答題
設數列{
an}的各項都是正數,且對任意
n∈N
*,都有
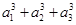
+…+
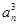
=
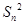
,記
Sn為數列{
an}的前
n項和.
(1)求數列{
an}的通項公式;
(2)若
bn=3
n+(-1)
n-1λ·2
an(
λ為非零常數,
n∈N
*),問是否存在整數
λ,使得對任意
n∈N
*,都有
bn+1>
bn.
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
已知正項數列{
an}滿足
a1=1,(
n+2)
an+12-(
n+1)
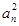
+
anan+1=0,則它的通項公式為( ).
查看答案和解析>>
科目:高中數學
來源:不詳
題型:單選題
已知數列{
an}的前
n項和
Sn滿足:
Sn+
Sm=
Sn+m,且
a1=1,那么
a11=( ).
查看答案和解析>>
主站蜘蛛池模板:
国产美女久久久
|
97精品国产
|
久久精品一区二区三区四区
|
亚洲国产二区
|
国产在线a|
国产欧美一区二区精品婷婷
|
久久精品久久久久久久久久久久久
|
超碰人人爽
|
欧美成人一区二免费视频软件
|
国产三级在线观看
|
日韩亚洲一区二区
|
日韩一区二区三区在线视频
|
99国产精品视频免费观看一公开
|
欧美激情精品久久久久久
|
av日韩一区|
99久久久久国产精品免费
|
欧洲三级在线
|
av电影网在线观看
|
日韩av在线中文字幕
|
久在线
|
可以看黄的视频
|
91精品久久久久久久久久入口
|
欧美日韩在线精品
|
av2014天堂网|
桃色视频国产
|
日韩精品无码一区二区三区
|
中文字幕乱码一区二区三区
|
欧美1级
|
亚洲第一免费视频网站
|
久久久99国产精品免费
|
国产aaa大片
|
色精品
|
爱福利视频
|
91精品国产92
|
成人a在线|
狠狠操狠狠操
|
亚洲欧洲中文日韩
|
国产精品久久久久久久久久东京
|
日韩久久久久久久久久久
|
国产免费黄视频
|
中文字幕在线一区二区三区
|

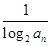 ,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整數k,使得
,Tn=bn+1+bn+2+…+b2n,是否存在最大的正整數k,使得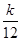 恒成立?若存在,求出k的值;若不存在,說明理由.
恒成立?若存在,求出k的值;若不存在,說明理由.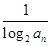 =
=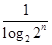 =
=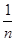 ,∴Tn=bn+1+bn+2+…+b2n=
,∴Tn=bn+1+bn+2+…+b2n=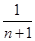 +
+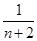 +…+
+…+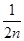 ,Tn+1=bn+2+bn+3+…+b2(n+1)=
,Tn+1=bn+2+bn+3+…+b2(n+1)=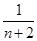 +
+ +…+
+…+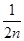 +
+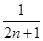 +
+ .
.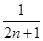 +
+ -
-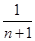 =
= =
= .
.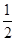 ,∴Tn≥T1=
,∴Tn≥T1=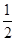 ,
,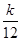 恒成立,則
恒成立,則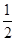 >
>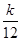 ,即k<6.又k是正整數,故存在最大正整數k=5使Tn>
,即k<6.又k是正整數,故存在最大正整數k=5使Tn>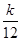 恒成立.
恒成立.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案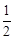 的等比數列{an}是遞減數列,其前n項和為Sn,且S1+a1,S2+a2,S3+a3成等差數列.
的等比數列{an}是遞減數列,其前n項和為Sn,且S1+a1,S2+a2,S3+a3成等差數列.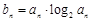 ,數列{bn}的前n項和Tn,求滿足不等式
,數列{bn}的前n項和Tn,求滿足不等式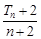 ≥
≥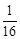 的最大n值.
的最大n值.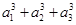 +…+
+…+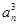 =
=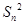 ,記Sn為數列{an}的前n項和.
,記Sn為數列{an}的前n項和.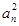 +anan+1=0,則它的通項公式為( ).
+anan+1=0,則它的通項公式為( ).