
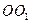 內(nèi)有一個三棱柱
內(nèi)有一個三棱柱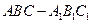 ,三棱柱的 底面為圓柱
,三棱柱的 底面為圓柱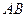 是圓
是圓 的直徑。
的直徑。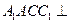 平面
平面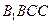 ;
;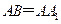 ,在圓
,在圓 柱
柱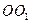 內(nèi)隨機選取一點,記該點取自三棱柱
內(nèi)隨機選取一點,記該點取自三棱柱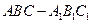 內(nèi)的概率為
內(nèi)的概率為 。
。 在圓周上運動時,求
在圓周上運動時,求 的最大值;
的最大值; 與平面
與平面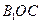 所成的角為
所成的角為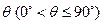 。當(dāng)
。當(dāng) 取最大值時,求
取最大值時,求
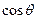 的值。
的值。
 平面ABC,
平面ABC, 平面ABC,所以
平面ABC,所以

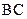 ,
,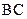

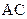 ,又
,又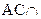
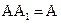 ,所以
,所以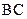
 平面
平面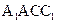 ,
, 平面
平面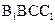 ,所以平面
,所以平面 平面
平面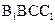 。
。 ,則AB=
,則AB= ,故三棱柱
,故三棱柱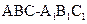 的體積為
的體積為 =
= ,
, ,
,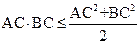 =
=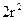 ,當(dāng)且僅當(dāng)
,當(dāng)且僅當(dāng) 時等號成立,
時等號成立, ,而圓柱的體積
,而圓柱的體積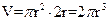 ,
, =
=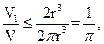 當(dāng)且僅當(dāng)
當(dāng)且僅當(dāng) ,即
,即 時等號成立,
時等號成立, 的最大值是
的最大值是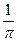 。
。 取最大值時,
取最大值時, ,于是以O(shè)為坐標(biāo)原點,建立空間直角坐標(biāo)系
,于是以O(shè)為坐標(biāo)原點,建立空間直角坐標(biāo)系 (如圖),則C(r,0,0),B(0,r,0),
(如圖),則C(r,0,0),B(0,r,0),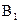 (
( 0,r,2r),
0,r,2r),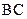
 平面
平面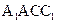 ,所以
,所以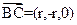 是平面
是平面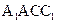 的一個法向量,
的一個法向量,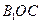 的法向量
的法向量 ,
, ,故
,故 ,
, 得平面
得平面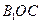 的一個法向量為
的一個法向量為 ,因為
,因為 ,
, 。
。

科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
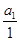 =
=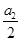 =
=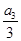 =k,則
=k,則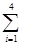 (ihi)=
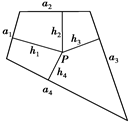
(ihi)=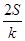 .類比以上性質(zhì),體積為V的三棱錐的第i個面的面積記為Si(i=1,2,3,4),此三棱錐內(nèi)任一點Q到第i個面的距離記為hi(i=1,2,3,4),若
.類比以上性質(zhì),體積為V的三棱錐的第i個面的面積記為Si(i=1,2,3,4),此三棱錐內(nèi)任一點Q到第i個面的距離記為hi(i=1,2,3,4),若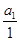 =
=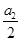 =
=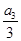 =K,則
=K,則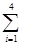 (ihi)=( )
(ihi)=( ) A. | B.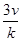 | C.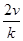 | D.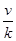 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
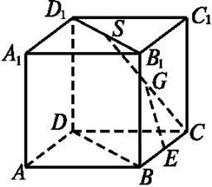
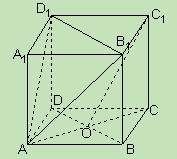
 本小題滿分12分)如圖,在三棱柱
本小題滿分12分)如圖,在三棱柱 中,
中,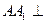 面
面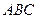 ,
,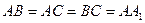 ,
,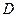 ,
,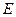 分別為
分別為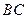 ,
,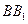
 的中點.
的中點.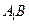 ∥平面
∥平面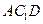 ; (2)求證:
; (2)求證: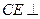 平面
平面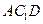 ;
;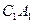 與平面
與平面 所成的角的
所成的角的 正弦值.
正弦值.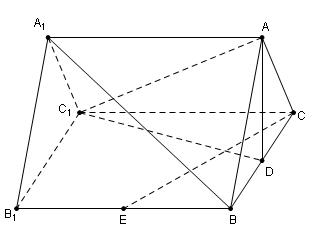
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.30° | B.45° | C. 75° | D.60° |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
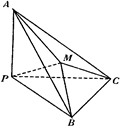
 為空間四點.在
為空間四點.在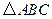 中,
中,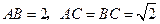 .等
.等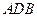 以
以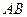 為軸運動.
為軸運動.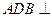 平面
平面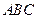 時,求
時,求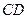 ;
;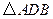 轉(zhuǎn)動時,是否總有
轉(zhuǎn)動時,是否總有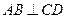 ?證明你的結(jié)論.
?證明你的結(jié)論.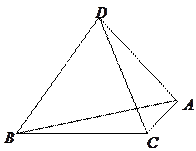
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
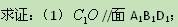
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
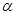 ,
,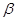 ,
,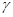 兩兩互相垂直,點
兩兩互相垂直,點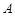 ∈
∈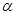 ,點
,點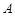 到
到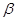 ,
,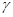 的距離都是
的距離都是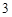 ,點
,點 是
是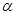 上的動點,滿足
上的動點,滿足 到
到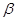 的距離是到
的距離是到 到點
到點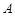 距離的
距離的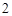 倍,則點
倍,則點 的軌跡上的點到
的軌跡上的點到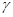 的距離的最小值是
的距離的最小值是A.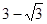 | B.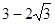 |
C.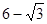 | D.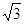 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
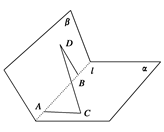
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com