
【題目】一緝私艇發現在方位角45°方向,距離12海里的海面上有一走私船正以10海里/小時的速度沿方位角為105°方向逃竄,若緝私艇的速度為14海里/小時,緝私艇沿方位角45°+α的方向追去,若要在最短的時間內追上該走私船,求追擊所需時間和α角的正弦.(注:方位角是指正北方向按順時針方向旋轉形成的角,設緝私艇與走私船原來的位置分別為A、C,在B處兩船相遇). 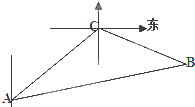
【答案】解:由條件知∠ACB=120°,AC=12海里,
設緝私船t小時后追上該走私船,可得BC=10t,AB=14t,
∴由正弦定理 ![]() =
= ![]() 得:
得: ![]() =
= ![]() ,
,
∴sinα= ![]() ,
,
由余弦定理AB2=AC2+BC2﹣2ACBCcos∠ACB得:(14t)2=122+(10t)2﹣240tcos120°,
解得:t=2或t=﹣ ![]() (舍),
(舍),
∴t=2小時,sinα= ![]() .
.
【解析】緝私艇與走私船原來的位置分別為A、C,在B處兩船相遇,由條件得到∠ACB=120°,AC=12海里,設緝私船t小時后追上該走私船,根據各自的速度表示出BC與AB,由∠ACB=120°,∠CAB=α,利用正弦定理列出關系式,求出sinα的值;由余弦定理列出關于t的方程,求出方程的解即可得到t的值.
【考點精析】通過靈活運用正弦定理的定義,掌握正弦定理:![]() 即可以解答此題.
即可以解答此題.


科目:高中數學 來源: 題型:
【題目】在一次愛心捐款活動中,小李為了了解捐款數額是否和居民自身的經濟收入有關,隨機調査了某地區的![]() 個捐款居民每月平均的經濟收入. 在捐款超過
個捐款居民每月平均的經濟收入. 在捐款超過![]() 元的居民中,每月平均的經濟收入沒有達到
元的居民中,每月平均的經濟收入沒有達到![]() 元的有
元的有![]() 個,達到
個,達到![]() 元的有
元的有![]() 個;在捐款不超過
個;在捐款不超過![]() 元的居民中,每月平均的經濟收入沒有達到
元的居民中,每月平均的經濟收入沒有達到![]() 元的有
元的有![]() 個.
個.
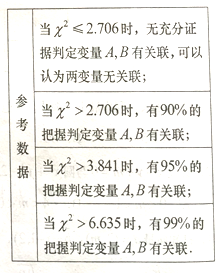
(1)在下圖表格空白處填寫正確數字,并說明是否有![]() 以上的把握認為捐款數額是否超過
以上的把握認為捐款數額是否超過![]() 元和居民毎月平均的經濟收入是否達到
元和居民毎月平均的經濟收入是否達到![]() 元有關?
元有關?
(2)將上述調查所得到的頻率視為概率. 現在從該地區大量居民中,采用隨機抽樣方法毎次抽取![]() 個居民,共抽取
個居民,共抽取![]() 次,記被抽取的
次,記被抽取的![]() 個居民中經濟收入達到
個居民中經濟收入達到![]() 元的人數為
元的人數為![]() ,求
,求![]() 和期望
和期望![]() 的值.
的值.
每月平均經濟收入達到 | 每月平均經濟收入沒有達到 | 合計 | |
捐款超過 | |||
捐款不超過 | |||
合計 |
附: 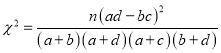 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
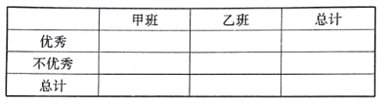
【題目】某中學數學老師分別用兩種不同教學方式對入學數學平均分和優秀率都相同的甲、乙兩個高一新班(人數均為20人)進行教學(兩班的學生學習數學勤奮程度和自覺性一致),數學期終考試成績莖葉圖如下:
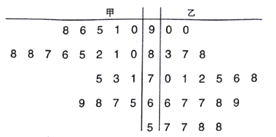
(1)學校規定:成績不低于75分的為優秀,請填寫下面的![]() 聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
聯表,并判斷有多大把握認為“成績優秀與教學方式有關”.
附:參考公式及數據

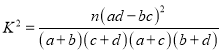
(2)從兩個班數學成績不低于90分的同學中隨機抽取3名,設![]() 為抽取成績不低于95分同學人數,求
為抽取成績不低于95分同學人數,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
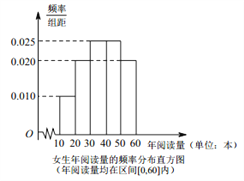
【題目】每年的4月23日為世界讀書日,為調查某高校學生(學生很多)的讀書情況,隨機抽取了男生,女生各20人組成的一個樣本,對他們的年閱讀量(單位:本)進行了統計,分析得到了男生年閱讀量的頻數分布表和女生年閱讀量的頻率分布直方圖.
男生年閱讀量的頻數分布表(年閱讀量均在區間![]() 內)
內)
![]()
(Ⅰ)根據女生年閱讀量的頻率分布直方圖估計該校女生年閱讀量的中位數;
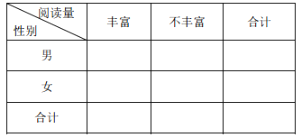
(Ⅱ)若年不小于40本為閱讀豐富,否則為閱讀不豐富,依據上述樣本研究年閱讀量與性別的關系,完成下列![]() 列聯表,并判斷是否有99%的把握認為閱讀豐富與性別有關;
列聯表,并判斷是否有99%的把握認為閱讀豐富與性別有關;
(Ⅲ)在樣本中,從年閱讀量在![]() 的學生中,隨機抽取2人參加全市的征文比賽,記這2人中男生人數為
的學生中,隨機抽取2人參加全市的征文比賽,記這2人中男生人數為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附: 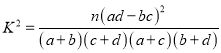 ,其中
,其中![]()

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某網站針對2015年中國好聲音歌手A,B,C三人進行網上投票,結果如下
觀眾年齡 | 支持A | 支持B | 支持C |
20歲以下 | 100 | 200 | 600 |
20歲以上(含20歲) | 100 | 100 | 400 |
(1)在所有參與該活動的人中,用分層抽樣的方法抽取n人,其中有6人支持A,求n的值.
(2)在支持C的人中,用分層抽樣的方法抽取5人作為一個總體,從這5人中任意選取2人,求恰有1人在20歲以下的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
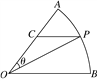
【題目】如圖所示,扇形AOB,圓心角AOB等于60°,半徑為2,在弧AB上有一動點P,過P引平行于OB的直線和OA交于點C,設∠AOP=θ,當△POC面積的最大值時θ的值為___________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Tn= ![]() n2﹣
n2﹣ ![]() n,且an+2+3log4bn=0(n∈N*)
n,且an+2+3log4bn=0(n∈N*)
(1)求{bn}的通項公式;
(2)數列{cn}滿足cn=anbn , 求數列{cn}的前n項和Sn;
(3)若cn≤ ![]() m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
m2+m﹣1對一切正整數n恒成立,求實數m的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com