
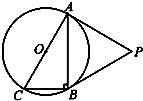
 如圖,⊙O是Rt△ABC的外接圓,∠ABC=90°,點P是圓外一點,PA切⊙O于點A,且PA=PB.
如圖,⊙O是Rt△ABC的外接圓,∠ABC=90°,點P是圓外一點,PA切⊙O于點A,且PA=PB.| 3 |
 ,
,| AP |
| DP |
| PO |
| PA |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| PO2-PA2 |


 開心蛙狀元作業系列答案
開心蛙狀元作業系列答案 課時掌控隨堂練習系列答案
課時掌控隨堂練習系列答案 一課一練一本通系列答案
一課一練一本通系列答案 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案科目:高中數學 來源: 題型:
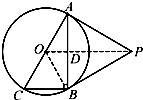
 (A)(幾何證明選講選做題)如圖,已知Rt△ABC的兩條直角邊AC,BC的長分別為3cm,4cm,以AC為直徑作圓與斜邊AB交于點D,則BD的長為=
(A)(幾何證明選講選做題)如圖,已知Rt△ABC的兩條直角邊AC,BC的長分別為3cm,4cm,以AC為直徑作圓與斜邊AB交于點D,則BD的長為=| 16 |
| 5 |
| 16 |
| 5 |
|
| π |
| 3 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
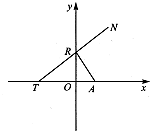 如圖所示,點A(p,o)(p>0),點R在y軸上運動,點T在x軸上,N為動點,且
如圖所示,點A(p,o)(p>0),點R在y軸上運動,點T在x軸上,N為動點,且| RT |
| RA |
| RN |
| RT |
| PM |
| QM |
查看答案和解析>>
科目:高中數學 來源:2011年高三數學精品復習10:定比分點、平移、正余弦定理(解析版) 題型:解答題
 ,BC=1,求⊙O的半徑.
,BC=1,求⊙O的半徑.
查看答案和解析>>
科目:高中數學 來源:2011年江蘇省蘇州市紅心中學高三摸底數學試卷(解析版) 題型:解答題
 ,BC=1,求⊙O的半徑.
,BC=1,求⊙O的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com