
【題目】設F1 , F2分別為橢圓 ![]() +y2=1的焦點,點A,B在橢圓上,若
+y2=1的焦點,點A,B在橢圓上,若 ![]() =5
=5 ![]() ;則點A的坐標是 .
;則點A的坐標是 .
【答案】(0,±1)
【解析】解:方法1:直線F1A的反向延長線與橢圓交于點B' 又∵ ![]()
由橢圓的對稱性,得 ![]()
設A(x1 , y1),B'(x2 , y2)
由于橢圓 ![]() 的a=
的a= ![]() ,b=1,c=
,b=1,c= ![]()
∴e= ![]() ,F1(
,F1( ![]() ,0).
,0).
∵|F1A|= ![]() |x1﹣
|x1﹣ ![]() |,
|,
|F1B'|= ![]() |x2﹣
|x2﹣ ![]() |,
|,
從而有: ![]() |x1﹣
|x1﹣ ![]() |=5×
|=5× ![]() |x2﹣
|x2﹣ ![]() |,
|,
由于 ![]() ≤x1 , x2
≤x1 , x2 ![]() ,
,
∴ ![]() ﹣x1>0,
﹣x1>0, ![]() ﹣x2>0,
﹣x2>0,
即 ![]() =5×
=5× ![]()
![]() =5
=5 ![]() . ①
. ①
又∵三點A,F1 , B′共線, ![]()
∴( ![]() ,y1﹣0)=5(﹣
,y1﹣0)=5(﹣ ![]() ﹣x2 , 0﹣y2)
﹣x2 , 0﹣y2)
∴ ![]() .②
.②
由①+②得:x1=0.
代入橢圓的方程得:y1=±1,
∴點A的坐標為(0,1)或(0,﹣1)
方法2:因為F1 , F2分別為橢圓 ![]() 的焦點,則
的焦點,則 ![]() ,
,
設A,B的坐標分別為A(xA , yA),B(xB , yB),
若 ![]() ;則
;則 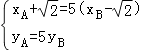 ,所以
,所以 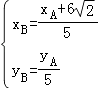 ,
,
因為A,B在橢圓上,所以 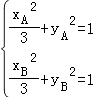 ,代入解得
,代入解得 ![]() 或
或 ![]() ,
,
故A(0,±1).
方法三、由e=| ![]() |,λ=5,e=
|,λ=5,e= ![]() ,cosθ=
,cosθ= ![]() ,sinθ=
,sinθ= ![]() ,
,
k=tanθ= ![]() ,由
,由 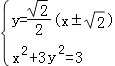 ,即可得到A(0,±1).
,即可得到A(0,±1).
所以答案是:(0,±1).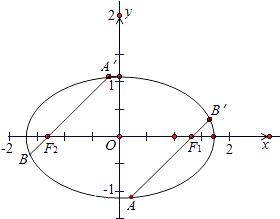


科目:高中數學 來源: 題型:
【題目】已知雙曲線 ![]() 的左、右焦點分別為F1、F2 , P為C的右支上一點,且|PF2|=|F1F2|,則
的左、右焦點分別為F1、F2 , P為C的右支上一點,且|PF2|=|F1F2|,則 ![]() 等于( )
等于( )
A.24
B.48
C.50
D.56
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設m,n∈R,定義在區間[m,n]上的函數f(x)=log2(4﹣|x|)的值域是[0,2],若關于t的方程( ![]() )|t|+m+1=0(t∈R)有實數解,則m+n的取值范圍是 .
)|t|+m+1=0(t∈R)有實數解,則m+n的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P﹣ABCD中,底面為直角梯形,AD∥BC,∠BAD=90°,PA⊥底面ABCD,PA=AD=AB=2BC,M,N分別為PC,PB的中點. (Ⅰ)求證:PB⊥DM;
(Ⅱ)求CD與平面ADMN所成的角的正弦值.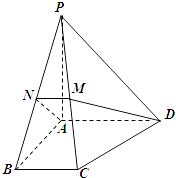
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量 ![]() =(2sinx,1),
=(2sinx,1), ![]() =(cosx,1﹣cos2x),函數f(x)=
=(cosx,1﹣cos2x),函數f(x)= ![]()
![]() (x∈R).
(x∈R).
(1)求函數f(x)的最小正周期、最大值和最小值;
(2)求函數f(x)的單調遞增區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】光明超市某種商品11月份(30天,11月1日為第一天)的銷售價格P(單位:元)與時間t(單位:天,其中)組成有序實數對(t,P),點(t,P)落在如圖所示的線段上.該商品日銷售量Q(單位:件)與時間t(單位:天,其中t∈N)滿足一次函數關系,Q與t的部分數據如表所示.
第t天 | 10 | 17 | 21 | 30 |
Q(件) | 180 | 152 | 136 | 100 |
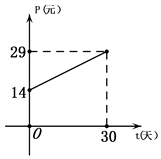
(1)根據圖象寫出銷售價格與時間t的函數關系式P=f(t).
(2)請根據表中數據寫出日銷售量Q與時間t的函數關系式Q=g(t).
(3)設日銷售額為M(單位:元),請求出這30天中第幾日M最大,最大值為多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)是定義在R上的偶函數,且當x>0時,f(x)=lg ![]() ,若對任意實數t∈[
,若對任意實數t∈[ ![]() ,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,則實數a的取值范圍 .
,2],都有f(t+a)﹣f(t﹣1)≥0恒成立,則實數a的取值范圍 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com