
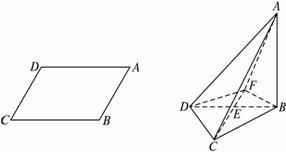
(1)證明AB⊥平面BCD;
(2)證明平面ACD⊥平面ABD;
(3)求二面角ACEB的大小.
解析:(1)證明:在△ABD中,由AB=a,AD=2a,∠A=60°,可得∠ABD=90°.?
又二面角A-BD-C為直二面角,AB![]() 面ABD,面ABD∩面BCD=DB,∴AB⊥平面BCD.?
面ABD,面ABD∩面BCD=DB,∴AB⊥平面BCD.?
(2)證明:由(1)知AB⊥平面BCD,CD![]() 平面BCD,?
平面BCD,?
∴AB⊥CD.?
同樣,仿(1)可證明CD⊥BD.?
而AB∩BD=B,∴CD⊥平面ABD.?
而CD![]() 平面ACD,∴平面ACD⊥平面ABD.?
平面ACD,∴平面ACD⊥平面ABD.?
(3)由(1)可得AB⊥平面BCD,過點B作BF⊥CE于F,連結AF,則由三垂線定理可得AF⊥CE.?
∴∠AFB即為二面角A-CE-B的平面角.?
由條件可得BF=![]() .?
.?
在△BFA中,tan∠BAF=![]() .?
.?
故二面角A-CE-B的大小為arctan![]() .
.


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
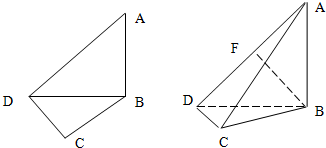 如圖,在平面四邊形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,現將四邊形ABCD沿BD折起,使平面ABD⊥平面BDC,設點F為棱AD的中點.
如圖,在平面四邊形ABCD中,已知∠A=45°,∠C=90°,∠ADC=105°,AB=BD,現將四邊形ABCD沿BD折起,使平面ABD⊥平面BDC,設點F為棱AD的中點.查看答案和解析>>
科目:高中數學 來源:全優設計必修四數學蘇教版 蘇教版 題型:022
在□ABCD中,已知A(-![]() ,-7),B(2,6),其對角線的交點M(3,
,-7),B(2,6),其對角線的交點M(3,![]() ),則C、D的坐標分別是________.
),則C、D的坐標分別是________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com