
【題目】如圖,已知△![]() 中,∠
中,∠![]() =90°,
=90°,![]() ,且
,且![]() =1,
=1,![]() =2,△
=2,△![]() 繞
繞![]() 旋轉至
旋轉至![]() ,使點
,使點![]() 與點
與點![]() 之間的距離
之間的距離![]() =
=![]() .
.
(1)求證:![]() ⊥平面
⊥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求異面直線![]() 與
與![]() 所成的角的余弦值.
所成的角的余弦值.

【答案】(1)見詳解;(2)60°;(3)![]() .
.
【解析】
(1)∵CD⊥AB,∴CD⊥A′D,CD⊥DB,∴CD⊥平面A′BD,
∴CD⊥BA′.又在△A′DB中,A′D=1,DB=2,A′B=![]()
,∴∠BA′D=90°,
即BA′⊥A′D,∴BA′⊥平面A′CD.
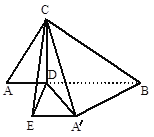
(2)∵CD⊥DB,CD⊥A′D,∴∠BDA′是二面角
A′—CD—B的平面角.又Rt△A′BD中,A′D=1,BD=2,
∴∠A′DB=60°,即 二面角A′—CD—B為60°.
(3)過A′作A′E∥BD,在平面A′BD中作DE⊥A′E于E,
連CE,則∠CA′E為A′C與BD所成角.
∵CD⊥平面A′BD,DE⊥A′E,∴A′E⊥CE.
∵EA′∥AB,∠A′DB=60°,∴∠DA′E=60°,又A′D=1,∠DEA′=90°,∴A′E=![]()
又∵在Rt△ACB中,AC=![]() =
=![]() ∴A′C=AC=
∴A′C=AC=![]()
∴cos∠CA′E=![]() =
=![]() =
=![]() ,即A′C與BD所成角的余弦值為
,即A′C與BD所成角的余弦值為![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 的圖象與x軸交點為
的圖象與x軸交點為![]() ,與此交點距離最小的最高點坐標為
,與此交點距離最小的最高點坐標為![]() .
.
(Ⅰ)求函數![]() 的表達式;
的表達式;
(Ⅱ)若函數![]() 滿足方程
滿足方程![]() ,求方程在
,求方程在![]() 內的所有實數根之和;
內的所有實數根之和;
(Ⅲ)把函數![]() 的圖像的周期擴大為原來的兩倍,然后向右平移
的圖像的周期擴大為原來的兩倍,然后向右平移![]() 個單位,再把縱坐標伸長為原來的兩倍,最后向上平移一個單位得到函數
個單位,再把縱坐標伸長為原來的兩倍,最后向上平移一個單位得到函數![]() 的圖像.若對任意的
的圖像.若對任意的![]() ,方程
,方程![]() 在區間
在區間![]() 上至多有一個解,求正數k的取值范圍.
上至多有一個解,求正數k的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ),且滿足
),且滿足![]() .
.
(1)求a的值;
(2)設函數![]() ,
,![]() (
(![]() ),若存在
),若存在![]() ,
,![]() ,使得
,使得![]() 成立,求實數t的取值范圍;
成立,求實數t的取值范圍;
(3)若存在實數m,使得關于x的方程![]() 恰有4個不同的正根,求實數m的取值范圍.
恰有4個不同的正根,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】我國古代數學家祖暅提出原理:“冪勢既同,則積不容異”.其中“冪”是截面積,“勢”是幾何體的高.原理的意思是:夾在兩個平行平面間的兩個幾何體,被任一平行于這兩個平行平面的平面所截,若所截的兩個截面的面積恒相等,則這兩個幾何體的體積相等.如圖所示,在空間直角坐標系![]() 的坐標平面
的坐標平面![]() 內,若函數
內,若函數 的圖象與
的圖象與![]() 軸圍成一個封閉區域
軸圍成一個封閉區域![]() ,將區域
,將區域![]() 沿
沿![]() 軸的正方向上移4個單位,得到幾何體如圖一.現有一個與之等高的圓柱如圖二,其底面積與區域
軸的正方向上移4個單位,得到幾何體如圖一.現有一個與之等高的圓柱如圖二,其底面積與區域![]() 面積相等,則此圓柱的體積為__________.
面積相等,則此圓柱的體積為__________.


查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】函數![]() 的部分圖象如圖所示,點A,B,C在圖象
的部分圖象如圖所示,點A,B,C在圖象![]() 上,
上,![]() ,
,![]() ,并且
,并且![]() 軸
軸
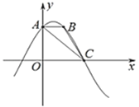
(1)求![]() 和
和![]() 的值及點B的坐標;
的值及點B的坐標;
(2)若![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)將函數![]() 的圖象上各點的縱坐標變為原來的
的圖象上各點的縱坐標變為原來的![]() 倍,橫坐標不變,再將所得圖象各點的橫坐標變為原來的
倍,橫坐標不變,再將所得圖象各點的橫坐標變為原來的![]() 倍,縱坐標不變,最后將所得圖象向右平移
倍,縱坐標不變,最后將所得圖象向右平移![]() 個單位,得到
個單位,得到![]() 的圖象,若關于x的方程
的圖象,若關于x的方程![]() 在區間
在區間![]() 上有兩個不同解,求實數a的取值范圍.
上有兩個不同解,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com