【題目】函數
有4個零點，其圖象如下圖，和圖象吻合的函數解析式是（ ）
A. 
B. 
C. 
D. 
【答案】D
【解析】根據圖像及零點的意義可知，圖像為兩個函數的交點，分別為
和
.
故
.
故選D.
得解：本函數圖象的交點、函數的零點、方程的根往往是“知一求二”，解答時要先判斷哪個好求解就轉化為哪個，判斷函數
零點個數的常用方法：(1) 直接法： 令
則方程實根的個數就是函數零點的個；(2) 零點存在性定理法：判斷函數在區間
上是連續不斷的曲線，且
再結合函數的圖象與性質(如單調性、奇偶性、周期性、對稱性) 可確定函數的零點個數；(3) 數形結合法：轉化為兩個函數的圖象的交點個數問題，畫出兩個函數的圖象，其交點的個數就是函數零點的個數，在一個區間上單調的函數在該區間內至多只有一個零點，在確定函數零點的唯一性時往往要利用函數的單調性，確定函數零點所在區間主要利用函數零點存在定理，有時可結合函數的圖象輔助解題.
科目：高中數學 來源： 題型：
【題目】某園林公司準備綠化一塊半徑為200米，圓心角為 
的扇形空地（如圖的扇形OPQ區域），扇形的內接矩形ABCD為一水池，其余的地方種花，若∠COP=α，矩形ABCD的面積為S（單位：平方米）．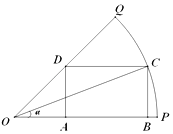 
（1）試將S表示為關于α的函數，求出該函數的表達式；
（2）角α取何值時，水池的面積 S最大，并求出這個最大面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知二次函數g（x）=mx2﹣2mx+n+1（m＞0）在區間[0，3]上有最大值4，最小值0．
（1）求函數g（x）的解析式；
（2）設f（x）= 
．若f（2x）﹣k2x≤0在x∈[﹣3，3]時恒成立，求k的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在直三棱柱ABC﹣A1B1C1中，三角形ABC為等腰直角三角形，AC=BC= 
，AA1=1，點D是AB的中點．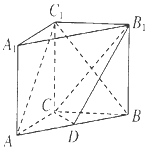 
（1）求證：AC1∥平面CDB1；
（2）二面角B1﹣CD﹣B的平面角的大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
