
【題目】已知拋物線![]() 與直線
與直線![]() 相交于A、B兩點.
相交于A、B兩點.
(1)求證:![]() ;
;
(2)當![]() 的面積等于
的面積等于![]() 時,求k的值.
時,求k的值.
【答案】解: (1) 當k = 0時直線與拋物線僅一個交點, 不合題意, ………… 2分
∴k 0由y =" k" (x+1)得x =![]() –1 代入y 2=" –" x 整理得: y 2+
–1 代入y 2=" –" x 整理得: y 2+![]() y – 1 =" 0" , 2分
y – 1 =" 0" , 2分
設A (x 1, y 1), B (x 2, y 2) 則y 1+ y 2= –![]() , y 1y 2=" –1." ………… 2分
, y 1y 2=" –1." ………… 2分
∵A、B在y 2=" –" x上, ∴A (–![]() , y 1), B (–
, y 1), B (–![]() , y 2) ,
, y 2) ,
∴ kOA·kOB=![]() =
=![]() =" –" 1 .
=" –" 1 .
∴ OA^OB. …………… 3 分
(2) 設直線與x軸交于E, 則 E ( – 1 , 0 ) ∴|OE| =" 1" ,
【解析】
試題(1)可假設![]() ,分別代入拋物線方程與直線方程,化簡整理可得
,分別代入拋物線方程與直線方程,化簡整理可得![]() ,
,![]() ,利用向量垂直有
,利用向量垂直有![]() ,即證明
,即證明![]() ;(2)直線
;(2)直線![]() 與
與![]() 軸的交點為
軸的交點為![]() 的坐標為
的坐標為![]() ,則可將三角形
,則可將三角形![]() 拆為兩個三角形
拆為兩個三角形![]() ,兩三角形具有相同的底邊
,兩三角形具有相同的底邊![]() ,高分別為
,高分別為![]() 的縱坐標,利用(1)中
的縱坐標,利用(1)中![]() 的關系便可求得
的關系便可求得![]() 的面積函數,根據函數值求
的面積函數,根據函數值求![]() 的值.
的值.
試題解析:(1)證明:聯立![]() ,消去x,得ky2+y-k=0.設A(x1,y1),B(x2,y2),則y1+y2=-
,消去x,得ky2+y-k=0.設A(x1,y1),B(x2,y2),則y1+y2=-![]() ,y1·y2=-1.因為y12=-x1,y22=-x2,所以(y1·y2)2=x1·x2,所以x1·x2=1,所以x1x2+y1y2=0,即
,y1·y2=-1.因為y12=-x1,y22=-x2,所以(y1·y2)2=x1·x2,所以x1·x2=1,所以x1x2+y1y2=0,即![]() =0,所以OA⊥OB.
=0,所以OA⊥OB.
(2)設直線l與x軸的交點為N,則N的坐標為(-1,0),
所以S△AOB=![]() |ON|·|y1-y2|
|ON|·|y1-y2|
=![]() ×|ON|×
×|ON|×![]()
=![]() ×1×
×1×![]() =
=![]() ,
,
解得k2=![]() ,所以k=±
,所以k=±![]() .
.


科目:高中數學 來源: 題型:
【題目】已知:等比數列{![]() }中,公比為q,且a1=2,a4=54,等差數列{
}中,公比為q,且a1=2,a4=54,等差數列{![]() }中,公差為d,b1=2,b1+b2+b3+b4=a1+ a2+ a3.
}中,公差為d,b1=2,b1+b2+b3+b4=a1+ a2+ a3.
(I)求數列{![]() }的通項公式;
}的通項公式;
(II)求數列{![]() }的前n項和
}的前n項和![]() 的公式;
的公式;
(III)設![]() ,
,![]() ,其中n=1,2,…,試比較
,其中n=1,2,…,試比較![]() 與
與![]() 的大小,并證明你的結論.
的大小,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某市民眾對某項公共政策的態度,在該市隨機抽取了![]() 名市民進行調查,做出了他們的月收入(單位:百元,范圍:
名市民進行調查,做出了他們的月收入(單位:百元,范圍:![]() )的頻率分布直方圖,同時得到他們月收入情況以及對該項政策贊成的人數統計表:
)的頻率分布直方圖,同時得到他們月收入情況以及對該項政策贊成的人數統計表:
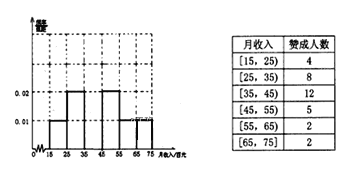
(1)求月收入在![]() 內的頻率,并補全這個頻率分布直方圖,并在圖中標出相應縱坐標;
內的頻率,并補全這個頻率分布直方圖,并在圖中標出相應縱坐標;
(2)根據頻率分布直方圖估計這![]() 人的平均月收入;
人的平均月收入;
(3)若從月收入(單位:百元)在![]() 的被調查者中隨機選取
的被調查者中隨機選取![]() 人,求
人,求![]() 人都不贊成的概率.
人都不贊成的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
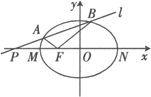
【題目】如圖,設![]() 是橢圓
是橢圓![]() 的左焦點,點
的左焦點,點![]() 是
是![]() 軸上的一點,點
軸上的一點,點![]() 為橢圓的左、右頂點,已知
為橢圓的左、右頂點,已知![]() ,且
,且![]()
(1)求橢圓的標準方程;
(2)過點![]() 作直線
作直線![]() 交橢圓于
交橢圓于![]() 兩點,試判定直線
兩點,試判定直線![]() 的斜率之和
的斜率之和![]() 是否為定值,并說明理由.
是否為定值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,已知C= ![]() ,向量
,向量 ![]() =(sinA,1),
=(sinA,1), ![]() =(1,cosB),且
=(1,cosB),且 ![]() .
.
(1)求A的值;
(2)若點D在邊BC上,且3 ![]() =
= ![]() ,
, ![]() =
= ![]() ,求△ABC的面積.
,求△ABC的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列{an}的前n項和為Sn , 且滿足Sn=2﹣an , n=1,2,3,….
(1)求數列{an}的通項公式;
(2)若數列{bn}滿足b1=1,且bn+1=bn+an , 求數列{bn}的通項公式;
(3)設cn= ![]() ,數列{cn}的前n項和為Tn=
,數列{cn}的前n項和為Tn= ![]() .求n.
.求n.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖所示,有一塊矩形空地ABCD,AB=2km,BC=4km,根據周邊環境及地形實際,當地政府規劃在該空地內建一個箏形商業區AEFG,箏形的頂點A,E,F,G為商業區的四個入口,其中入口F在邊BC上(不包含頂點),入口E,G分別在邊AB,AD上,且滿足點A,F恰好關于直線EG對稱,矩形內箏形外的區域均為綠化區. 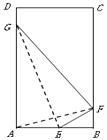
(1)請確定入口F的選址范圍;
(2)設商業區的面積為S1 , 綠化區的面積為S2 , 商業區的環境舒適度指數為 ![]() ,則入口F如何選址可使得該商業區的環境舒適度指數最大?
,則入口F如何選址可使得該商業區的環境舒適度指數最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點A(0,-2),橢圓E: ![]() (a>b>0)的離心率為
(a>b>0)的離心率為![]() ,F是橢圓E的右焦點,直線AF的斜率為
,F是橢圓E的右焦點,直線AF的斜率為![]() ,O為坐標原點.
,O為坐標原點.
(1)求E的方程;
(2)設過點A的動直線l與E相交于P,Q兩點.當△OPQ的面積最大時,求l的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com