

 PA,求二面角D-BC-A的大小;(結果用反三角函數值表示)
PA,求二面角D-BC-A的大小;(結果用反三角函數值表示)| 解:(1)∵棱臺DEF-ABC與棱錐P-ABC的棱長和相等, ∴DE+EF+FD=PD+OE+PF 又∵截面DEF∥底面ABC, ∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°, ∴P-ABC是正四面體。 |
|
| (2)取BC的中點M,連接PM,DM,AM ∵BC⊥PM,BC⊥AM, ∴BC⊥平面PAM,BC⊥DM, 則∠DMA為二面角D-BC-A的平面角 由(1)知,P-ABC的各棱長均為1, ∴PM=AM= 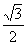 ,由D是PA的中點,得 ,由D是PA的中點,得 sin∠DMA= 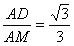 , ,∴∠DMA=arcsin 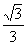 。 。 |
 |
| (3)存在滿足條件的直平行六面體 棱臺DEF-ABC的棱長和為定值6,體積為V 設直平行六面體的棱長均為 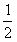 ,底面相鄰兩邊夾角為α, ,底面相鄰兩邊夾角為α, 則該六面體棱長和為6,體積為 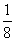 sinα=V sinα=V∵正四面體P-ABC的體積是 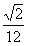 , ,∴0<V< 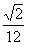 ,0<8V<1 ,0<8V<1可知α=arcsim(8V) 故構造棱長均為 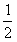 ,底面相鄰兩邊夾角為arcsim(8V)的直平行六面體即滿足要求。 ,底面相鄰兩邊夾角為arcsim(8V)的直平行六面體即滿足要求。 |


 名師導航單元期末沖刺100分系列答案
名師導航單元期末沖刺100分系列答案 名校名卷單元同步訓練測試題系列答案
名校名卷單元同步訓練測試題系列答案科目:高中數學 來源: 題型:
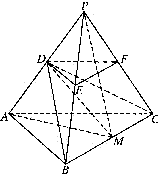
 如圖,P-ABC是底面邊長為1的正三棱錐,D、E、F分別為棱長PA、PB、PC上的點,截面DEF∥底面ABC,且棱臺DEF-ABC與棱錐P-ABC的棱長和相等.(棱長和是指多面體中所有棱的長度之和)
如圖,P-ABC是底面邊長為1的正三棱錐,D、E、F分別為棱長PA、PB、PC上的點,截面DEF∥底面ABC,且棱臺DEF-ABC與棱錐P-ABC的棱長和相等.(棱長和是指多面體中所有棱的長度之和)| 1 | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 如圖,P-ABC是底面邊長為1的正三棱錐,D、E、F分別為棱長PA、PB、PC上的點,截面DEF∥底面ABC,且棱臺DEF-ABC與棱錐P-ABC的棱長和相等.(棱長和是指多面體中所有棱的長度之和)
如圖,P-ABC是底面邊長為1的正三棱錐,D、E、F分別為棱長PA、PB、PC上的點,截面DEF∥底面ABC,且棱臺DEF-ABC與棱錐P-ABC的棱長和相等.(棱長和是指多面體中所有棱的長度之和) 求二面角D-BC-A的大小;(結果用反三角函數值表示)
求二面角D-BC-A的大小;(結果用反三角函數值表示)查看答案和解析>>
科目:高中數學 來源:2004年上海市高考數學試卷(文科)(解析版) 題型:解答題
 求二面角D-BC-A的大小;(結果用反三角函數值表示)
求二面角D-BC-A的大小;(結果用反三角函數值表示)
查看答案和解析>>
科目:高中數學 來源:2004年上海市高考數學試卷(理科)(解析版) 題型:解答題
 求二面角D-BC-A的大小;(結果用反三角函數值表示)
求二面角D-BC-A的大小;(結果用反三角函數值表示)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com