【題目】已知
是等差數列， 
是等比數列， 
， 
， 
， 
.
（1）求
， 
的通項公式；
（2）
的前
項和為
，求證： 
.
【答案】（1）
， 
；（2）見解析
【解析】試題分析：（1）根據
是等差數列， 
是等比數列， 
， 
， 
， 
列出關于公比
、公差
的方程組，解方程組可得
與
的值，從而可得數列
， 
的通項公式；（2）由（1）可知
，根據錯位相減法結合等比數列的求和公式可得
的前
項和為
，利用放縮法可得結論.
試題解析：（1）設
公差為
， 
公比為
，
由題意得： 
，
解得
，或
（舍），
∴
， 
.
（2）
，
，
相減得： 
，
∴
，∴
.
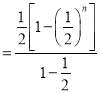
【 方法點睛】本題主要考查等比數列和等差數列的通項以及錯位相減法求數列的前
項和，屬于中檔題.一般地，如果數列
是等差數列， 
是等比數列，求數列
的前
項和時，可采用“錯位相減法”求和，一般是和式兩邊同乘以等比數列
的公比，然后作差求解, 在寫出“
”與“
” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“
”的表達式.
科目：高中數學 來源： 題型：
【題目】如圖，矩形ADEF與梯形ABCD所在的平面互相垂直，
，
，
，
，
，M為CE的中點，N為CD中點．
求證：平面
平面ADEF；
求證：平面
平面BDE；
求點D到平面BEC的距離．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在四棱錐P-ABCD中，△PBC為正三角形，AB⊥平面PBC，AB∥CD，AB=
DC， 
.
(1)求證：AE∥平面PBC；
(2)求證：AE⊥平面PDC.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】高鐵是我國國家名片之一，高鐵的修建凝聚著中國人的智慧與汗水.如圖所示，B、E、F為山腳兩側共線的三點，在山頂A處測得這三點的俯角分別為
、
、
，計劃沿直線BF開通穿山隧道，現已測得BC、DE、EF三段線段的長度分別為3、1、2.
（1）求出線段AE的長度；
（2）求出隧道CD的長度.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】數列{an}為遞增的等差數列，數列{bn}滿足bn＝anan+1an+2（n∈N*），設Sn為數列{bn}的前n項和，若a2
，則當Sn取得最小值時n的值為（ ）
A.14B.13C.12D.11
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現安排甲、乙、丙、丁、戊5名同學參加2022年杭州亞運會志愿者服務活動，有翻譯、導游、禮儀、司機四項工作可以安排，以下說法正確的是（ ）
A. 每人都安排一項工作的不同方法數為
B. 每項工作至少有一人參加，則不同的方法數為
C. 如果司機工作不安排，其余三項工作至少安排一人，則這5名同學全部被安排的不同方法數為
D. 每項工作至少有一人參加，甲、乙不會開車但能從事其他三項工作，丙、丁、戊都能勝任四項工作，則不同安排方案的種數是
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法中正確的個數是( )
(1) 已知
，
，
，則
(2)將6個相同的小球放入4個不同的盒子中，要求不出現空盒，共有10種放法．
(3) 
被
除后的余數為
．
(4) 若
，則
＝
(5)拋擲兩個骰子，取其中一個的點數為點
的橫坐標，另一個的點數為點的縱坐標，連續拋擲這兩個骰子三次，點在圓
內的次數
的均值為
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】下列說法正確的是( )
A. 若命題
都是真命題,則命題“
”為真命題
B. 命題“
”的否定是“
,
”
C. 命題:“若
,則
或
”的否命題為“若
,則
或
”
D. “
”是“
”的必要不充分條件
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數
（1）令
，試討論
的單調性；
（2）若對
恒成立,求
的取值范圍.
【答案】（1）見解析（2）
【解析】試題分析：（1）由
，對函數求導，研究導函數的正負得到單調性即可；（2）由條件可知
對
恒成立，變量分離
，令
，求這個函數的最值即可.
解析：
（1）由
得
當
時， 
恒成立，則
單調遞減；
當
時， 
，令
，
令
.
綜上：當
時， 
單調遞減，無增區間；
當
時， 
， 
（2）由條件可知
對
恒成立，則
當
時， 
對
恒成立
當
時，由
得
.令
則
,因為
,所以
,即
所以
,從而可知
.
綜上所述: 所求
.
點睛：導數問題經常會遇見恒成立的問題：
（1）根據參變分離，轉化為不含參數的函數的最值問題；
（2）若 
就可討論參數不同取值下的函數的單調性和極值以及最值，最終轉化為
，若
恒成立
；
（3）若
恒成立，可轉化為
（需在同一處取得最值） .
【題型】解答題
【結束】
22
【題目】在平面直角坐標系
中，曲線
的參數方程為
(
為參數），以
為極點， 
軸的非負半軸為極軸的極坐標系中，直線
的極坐標方程為
.
（1）求曲線
的極坐標方程；
（2）設直線
與曲線
相交于
兩點，求
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com