【答案】
分析:利用二倍角公式求出2sin15°cos15°,sin
215°-cos
215°,1-2sin
215°的值,利用同角三角函數的基本關系式求出sin
215°+cos
215°的值,即可得到選項.
解答:解:因為2sin15°cos15°=sin30°=

,sin
215°-cos
215°=-cos30°=-
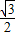
,1-2sin
215°=cos30°=

;sin
215°+cos
215°=1;所以1-2sin
215°的值為:
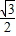
;
故選C.
點評:本題考查三角函數的二倍角公式的應用,同角三角函數的基本關系式的應用,特殊角的三角函數值,基礎題.

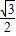 的是( )
的是( )