
【題目】已知單調遞增的等比數列![]() 滿足:
滿足: ![]() ,
, ![]()
(1)求數列![]() 的通項公式;
的通項公式;
(2)若![]() ,數列
,數列![]() 的前
的前![]() 項和為
項和為![]() ,
, ![]() 成立的正整數
成立的正整數![]() 的最小值.
的最小值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】試題分析:(1)(1)根據等比數列![]() 滿足:
滿足: ![]() ,
, ![]() 列出關于首項
列出關于首項![]() 、公差
、公差![]() 的方程組,解方程組可得
的方程組,解方程組可得![]() 與
與![]() 的值,從而可得數列
的值,從而可得數列![]() 的通項公式;(2)先求數列
的通項公式;(2)先求數列![]() 的通項公式,利用錯位相減法求得前
的通項公式,利用錯位相減法求得前![]() 項和為
項和為![]() ,將
,將![]() 再代入
再代入![]() 整理,解不等式即可求出
整理,解不等式即可求出![]() 成立的正整數
成立的正整數![]() 的最小值.
的最小值.
試題解析:(1)設等比例列![]() 的首項為
的首項為![]() ,公比為q
,公比為q
依題意,有![]() ,解之得
,解之得![]() 或
或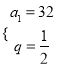 ,
,
又數列![]() 單調遞增,
單調遞增, ![]()
(2)依題意, ![]()
![]() ①
①
![]() ②
②
由①—②得: ![]()
![]()
![]() ,
, ![]() ,即
,即![]() ,
, ![]() 當
當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,
, ![]() 使
使![]() ,成立的正整數
,成立的正整數![]() 的最小值為
的最小值為![]() .
.
【 方法點睛】本題主要考查等比數列的通項公式與求和公式以及錯位相減法求數列的的前![]() 項和,屬于中檔題.一般地,如果數列
項和,屬于中檔題.一般地,如果數列![]() 是等差數列,
是等差數列, ![]() 是等比數列,求數列
是等比數列,求數列![]() 的前
的前![]() 項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列
項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列![]() 的公比,然后作差求解, 在寫出“
的公比,然后作差求解, 在寫出“![]() ”與“
”與“![]() ” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“
” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“![]() ”的表達式.
”的表達式.


科目:高中數學 來源: 題型:
【題目】如圖,設拋物線![]() 的準線
的準線![]() 與
與![]() 軸交于橢圓
軸交于橢圓![]() 的右焦點
的右焦點![]() 為
為![]() 的左焦點.橢圓的離心率為
的左焦點.橢圓的離心率為![]() ,拋物線
,拋物線![]() 與橢圓
與橢圓![]() 交于
交于![]() 軸上方一點
軸上方一點![]() ,連接
,連接![]() 并延長其交
并延長其交![]() 于點
于點![]() ,
, ![]() 為
為![]() 上一動點,且在
上一動點,且在![]() 之間移動.
之間移動.
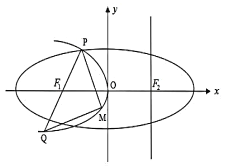
(1)當![]() 取最小值時,求
取最小值時,求![]() 和
和![]() 的方程;
的方程;
(2)若![]() 的邊長恰好是三個連續的自然數,當
的邊長恰好是三個連續的自然數,當![]() 面積取最大值時,求面積最大值以及此時直線
面積取最大值時,求面積最大值以及此時直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}前n項和Sn滿足:2Sn+an=1
(1)求數列{an}的通項公式;
(2)設bn= ![]() ,數列{bn}的前n項和為Tn , 求證:Tn<
,數列{bn}的前n項和為Tn , 求證:Tn< ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定點![]() ,定直線
,定直線![]() :
: ![]() ,動圓
,動圓![]() 過點
過點![]() ,且與直線
,且與直線![]() 相切.
相切.
(Ⅰ)求動圓![]() 的圓心軌跡
的圓心軌跡![]() 的方程;
的方程;
(Ⅱ)過點![]() 的直線與曲線
的直線與曲線![]() 相交于
相交于![]() ,
, ![]() 兩點,分別過點
兩點,分別過點![]() ,
, ![]() 作曲線
作曲線![]() 的切線
的切線![]() ,
, ![]() ,兩條切線相交于點
,兩條切線相交于點![]() ,求
,求![]() 外接圓面積的最小值.
外接圓面積的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】自2016年下半年起六安市區商品房價不斷上漲,為了調查研究六安城區居民對六安商品房價格承受情況,寒假期間小明在六安市區不同小區分別對50戶居民家庭進行了抽查,并統計出這50戶家庭對商品房的承受價格(單位:元/平方),將收集的數據分成![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 五組(單位:元/平方),并作出頻率分布直方圖如圖:
五組(單位:元/平方),并作出頻率分布直方圖如圖:
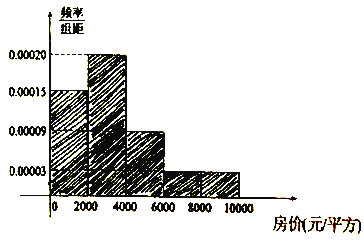
(Ⅰ)試根據頻率分布直方圖估計出這50戶家庭對商品房的承受價格平均值(單位:元/平方);
(Ⅱ)為了作進一步調查研究,小明準備從承受能力超過4000元/平方的居民中隨機抽出2戶進行再調查,設抽出承受能力超過8000元/平方的居民為![]() 戶,求
戶,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com