
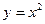 在
在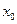 到
到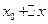 的平均變化率為
的平均變化率為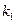 ,在
,在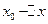 到
到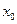 的平均變化率為
的平均變化率為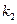 ,則二者的大小關(guān)系是 .
,則二者的大小關(guān)系是 .科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 為
為 ,射線
,射線 為
為 ,動點
,動點 在
在 的內(nèi)部,
的內(nèi)部, 于
于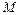 ,
, 于
于 ,四邊形
,四邊形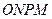 的面積恰為
的面積恰為 .
. 為定值時,動點
為定值時,動點 的縱坐標(biāo)
的縱坐標(biāo) 是橫坐標(biāo)
是橫坐標(biāo) 的函數(shù),求這個函數(shù)
的函數(shù),求這個函數(shù) 的解析式;
的解析式; 的取值范圍,確定
的取值范圍,確定 的定義域.
的定義域. |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
 萬元的一條流水線,要提高該流水線的生產(chǎn)能力,就要對其進(jìn)行技術(shù)改造,從而提高產(chǎn)品附加值,改造需要投入,假設(shè)附加值
萬元的一條流水線,要提高該流水線的生產(chǎn)能力,就要對其進(jìn)行技術(shù)改造,從而提高產(chǎn)品附加值,改造需要投入,假設(shè)附加值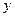 萬元與技術(shù)改造投入
萬元與技術(shù)改造投入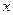 萬元之間的關(guān)系滿足:①
萬元之間的關(guān)系滿足:①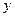 與
與 和
和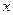 的乘積成正比;②
的乘積成正比;②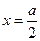 時,
時, ;③
;③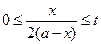 ,其中
,其中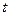 為常數(shù),且
為常數(shù),且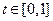 。
。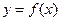 ,求
,求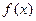 表達(dá)式,并求
表達(dá)式,并求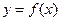 的定義域;
的定義域; 的最大值,并求出此時的技術(shù)改造投入。
的最大值,并求出此時的技術(shù)改造投入。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:解答題
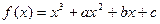 的圖象過原點,且在x=1處取得極值,直線
的圖象過原點,且在x=1處取得極值,直線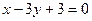 與曲線
與曲線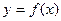 在原點處的切線互相垂直。
在原點處的切線互相垂直。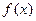 的解析式;
的解析式;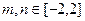 ,恒有
,恒有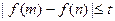 成立,求實數(shù)t的取值范圍。
成立,求實數(shù)t的取值范圍。查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com