從數列{an}中取出部分項,并將它們按原來的順序組成一個數列,稱之為數列{an}的一個子數列.設數列{an}是一個首項為a1、公差為d(d≠0)的無窮等差數列.
(1)若a1,a2,a5成等比數列,求其公比q.
(2)若a1=7d,從數列{an}中取出第2項、第6項作為一個等比數列的第1項、第2項,試問該數列是否為{an}的無窮等比子數列,請說明理由.
(3)若a1=1,從數列{an}中取出第1項、第m(m≥2)項(設am=t)作為一個等比數列的第1項、第2項,試問當且僅當t為何值時,該數列為{an}的無窮等比子數列,請說明理由.
【答案】
分析:(1)由題設知(a
1+d)
2=a
1(a
1+4d),由此可求出其公比
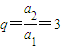
.
(2)設等比數列為{b
m},其公比
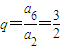
,
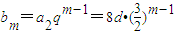
,由題設a
n=a
1+(n-1)d=(n+6)d.再由反證法能夠推出該數列不為{a
n}的無窮等比子數列.
(3)①設{a
n}的無窮等比子數列為{b
r},其公比
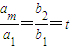
(t≠1),得b
r=t
r-1,由此入手能夠推導出t是大于1的正整數.
②再證明:若t是大于1的正整數,則數列{a
n}存在無窮等比子數列.即證明無窮等比數列{b
r}中的每一項均為數列{a
n}中的項.綜上,當且僅當t是大于1的正整數時,數列{a
n}存在無窮等比子數列.
解答:解:(1)由題設,得a
22=a
1a
5,即(a
1+d)
2=a
1(a
1+4d),得d
2=2a
1d,又d≠0,
于是d=2a
1,故其公比
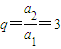
.
(2)設等比數列為{b
m},其公比
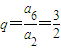
,
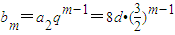
,
由題設a
n=a
1+(n-1)d=(n+6)d.
假設數列{b
m}為{a
n}的無窮等比子數列,
則對任意自然數m(m≥3),都存在n∈N
*,使a
n=b
m,
即

,
得
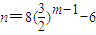
,
當m=5時,
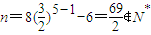
,與假設矛盾,
故該數列不為{a
n}的無窮等比子數列.
(3)①設{a
n}的無窮等比子數列為{b
r},其公比
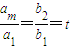
(t≠1),得b
r=t
r-1,
由題設,在等差數列{a
n}中,
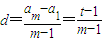
,
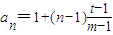
,
因為數列{b
r}為{a
n}的無窮等比子數列,
所以對任意自然數r(r≥3),都存在n∈N
*,使a
n=b
r,
即

,
得

,
由于上式對任意大于等于3的正整數r都成立,且n,m-1均為正整數,
可知t
r-2+t
r-3+t+1必為正整數,
又d≠0,
故t是大于1的正整數.
②再證明:若t是大于1的正整數,則數列{a
n}存在無窮等比子數列.
即證明無窮等比數列{b
r}中的每一項均為數列{a
n}中的項.
在等比數列{b
r}中,b
r=t
r-1,
在等差數列{a
n}中,
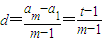
,
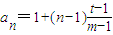
,
若b
r為數列{a
n}中的第k項,則由b
r=a
k,得
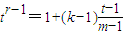
,
整理得

,
由t,m-1均為正整數,得k也為正整數,
故無窮等比數列{b
r}中的每一項均為數列{a
n}中的項,得證.
綜上,當且僅當t是大于1的正整數時,數列{a
n}存在無窮等比子數列.
點評:本題考查數列的綜合運用,難度較大,解題時要認真審題,仔細解答,避免出錯.

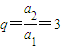 .
.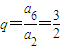 ,
,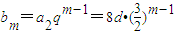 ,由題設an=a1+(n-1)d=(n+6)d.再由反證法能夠推出該數列不為{an}的無窮等比子數列.
,由題設an=a1+(n-1)d=(n+6)d.再由反證法能夠推出該數列不為{an}的無窮等比子數列.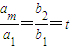 (t≠1),得br=tr-1,由此入手能夠推導出t是大于1的正整數.
(t≠1),得br=tr-1,由此入手能夠推導出t是大于1的正整數.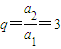 .
.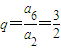 ,
,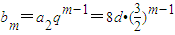 ,
, ,
,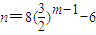 ,
,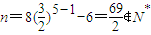 ,與假設矛盾,
,與假設矛盾,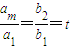 (t≠1),得br=tr-1,
(t≠1),得br=tr-1,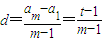 ,
,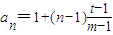 ,
, ,
, ,
,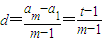 ,
,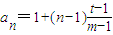 ,
,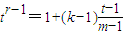 ,
, ,
,

 學習實踐園地系列答案
學習實踐園地系列答案