
| A.命題“若m > 0,則方程x2+x-m=0有實數(shù)根”的逆否命題為:“若方程x2+x-m=0無實數(shù)根,則m≤0”. |
| B.“x=1”是“x2-3x + 2=0”的充分不必要條件. |
C.若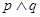 為假命題,則p ,q均為假命題. 為假命題,則p ,q均為假命題. |
D.對于命題p: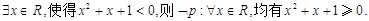 |


科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
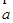 ∥
∥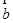
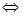 存在唯一的實數(shù)
存在唯一的實數(shù)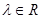 ,使得
,使得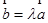 ;
;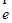 為單位向量,且
為單位向量,且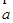 ∥
∥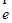 ,則
,則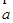 =±|
=±|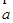 |·
|·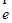 ;③
;③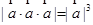 ;
;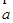 與
與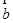 共線,
共線,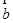 與
與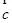 共線,則
共線,則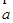 與
與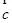 共線;⑤若
共線;⑤若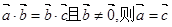
| A.①⑤ | B.②③④ |
| C.②③ | D.①④⑤ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
| A.逆命題為“單調(diào)函數(shù)不是周期函數(shù)” | B.否命題為“周期函數(shù)是單調(diào)函數(shù)” |
| C.逆否命題為“單調(diào)函數(shù)是周期函數(shù)” | D.以上三者都不對 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
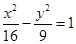 與橢圓
與橢圓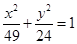 有相同的焦點;
有相同的焦點;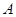 、
、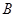 為兩個定點,
為兩個定點,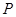 為動點,且
為動點,且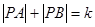 ,其中常數(shù)
,其中常數(shù)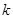 為正實數(shù),則動點
為正實數(shù),則動點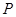 的軌跡為橢圓;
的軌跡為橢圓;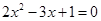 的兩根可分別作為橢圓和雙曲線的離心率;
的兩根可分別作為橢圓和雙曲線的離心率;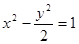 的右焦點
的右焦點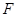 作直線
作直線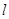 交雙曲線于
交雙曲線于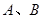 兩點,若
兩點,若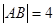 ,則這樣的直線
,則這樣的直線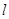 有且僅有3條。
有且僅有3條。查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:填空題
 ,其中
,其中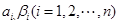 均為常數(shù),下列說法正確的有
均為常數(shù),下列說法正確的有 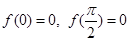 ,則對于任意
,則對于任意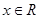 ,
,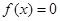 恒成立;
恒成立;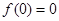 ,則
,則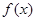 是奇函數(shù); (3) 若
是奇函數(shù); (3) 若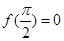 ,則
,則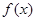 是偶函數(shù);(4) 若
是偶函數(shù);(4) 若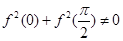 ,且當
,且當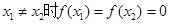 ,則
,則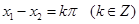 ;
;查看答案和解析>>
科目:高中數(shù)學(xué) 來源:不詳 題型:單選題
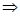 a∈A∪B ②A
a∈A∪B ②A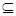 B
B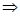 A∪B=B ③a∈B
A∪B=B ③a∈B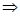 a∈A∩B ④A∪B="B"
a∈A∩B ④A∪B="B" 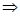 A∩B =A⑤A∪B=B∪C
A∩B =A⑤A∪B=B∪C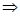 A=C
A=C| A.2 | B.3 | C.4 | D.5 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com