
【題目】2015男籃亞錦賽決賽階段,中國(guó)男籃以![]() 連勝的不敗成績(jī)贏得第
連勝的不敗成績(jī)贏得第![]() 屆亞錦賽冠軍,同時(shí)拿到亞洲唯一
屆亞錦賽冠軍,同時(shí)拿到亞洲唯一![]() 張直通里約奧運(yùn)會(huì)的入場(chǎng)券.賽后,中國(guó)男籃主力易建聯(lián)榮膺本屆亞錦賽
張直通里約奧運(yùn)會(huì)的入場(chǎng)券.賽后,中國(guó)男籃主力易建聯(lián)榮膺本屆亞錦賽![]() (最有價(jià)值球員),下表是易建聯(lián)在這
(最有價(jià)值球員),下表是易建聯(lián)在這![]() 場(chǎng)比賽中投籃的統(tǒng)計(jì)數(shù)據(jù).
場(chǎng)比賽中投籃的統(tǒng)計(jì)數(shù)據(jù).
比分 | 易建聯(lián)技術(shù)統(tǒng)計(jì) | |||
投籃命中 | 罰球命中 | 全場(chǎng)得分 | 真實(shí)得分率 | |
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
中國(guó) |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真實(shí)得分率)是衡量球員進(jìn)攻的效率,其計(jì)算公式為:
(真實(shí)得分率)是衡量球員進(jìn)攻的效率,其計(jì)算公式為:
![]()
(1)從上述![]() 場(chǎng)比賽中隨機(jī)選擇一場(chǎng),求易建聯(lián)在該場(chǎng)比賽中
場(chǎng)比賽中隨機(jī)選擇一場(chǎng),求易建聯(lián)在該場(chǎng)比賽中![]() 超過(guò)
超過(guò)![]() 的概率;
的概率;
(2)我們把比分分差不超過(guò)![]() 分的比賽稱(chēng)為“膠著比賽”.為了考驗(yàn)求易建聯(lián)在“膠著比賽”中的發(fā)揮情況,從“膠著比賽”中隨機(jī)選擇兩場(chǎng),求易建聯(lián)在這兩場(chǎng)比賽中
分的比賽稱(chēng)為“膠著比賽”.為了考驗(yàn)求易建聯(lián)在“膠著比賽”中的發(fā)揮情況,從“膠著比賽”中隨機(jī)選擇兩場(chǎng),求易建聯(lián)在這兩場(chǎng)比賽中![]() 至少有一場(chǎng)超過(guò)
至少有一場(chǎng)超過(guò)![]() 的概率;
的概率;
(3)用![]() 來(lái)表示易建聯(lián)某場(chǎng)的得分,用
來(lái)表示易建聯(lián)某場(chǎng)的得分,用![]() 來(lái)表示中國(guó)隊(duì)該場(chǎng)的總分,畫(huà)出散點(diǎn)圖如圖所示,請(qǐng)根據(jù)散點(diǎn)圖判斷
來(lái)表示中國(guó)隊(duì)該場(chǎng)的總分,畫(huà)出散點(diǎn)圖如圖所示,請(qǐng)根據(jù)散點(diǎn)圖判斷![]() 與
與![]() 之間是否具有線性相關(guān)關(guān)系?結(jié)合實(shí)際簡(jiǎn)單說(shuō)明理由.
之間是否具有線性相關(guān)關(guān)系?結(jié)合實(shí)際簡(jiǎn)單說(shuō)明理由.

【答案】(1)![]() (2)
(2)![]() (3)不具有線性相關(guān)關(guān)系
(3)不具有線性相關(guān)關(guān)系
【解析】試題分析:(1)由已知,結(jié)合古典概型計(jì)算公式可得:易建聯(lián)在該場(chǎng)比賽中![]() 超過(guò)
超過(guò)![]() 的概率。(2)由已知,結(jié)合古典概型計(jì)算公式可得:易建聯(lián)在兩場(chǎng)比賽中
的概率。(2)由已知,結(jié)合古典概型計(jì)算公式可得:易建聯(lián)在兩場(chǎng)比賽中![]() 超過(guò)
超過(guò)![]() 的概率。(3)根據(jù)散點(diǎn)圖,并不是分布在某一條直線的周?chē)傻媒Y(jié)論。
的概率。(3)根據(jù)散點(diǎn)圖,并不是分布在某一條直線的周?chē)傻媒Y(jié)論。
(1)設(shè)易建聯(lián)在比賽中![]() 超過(guò)
超過(guò)![]() 為事件
為事件![]() ,則共有
,則共有![]() 場(chǎng)比賽中
場(chǎng)比賽中![]() 超過(guò)
超過(guò)![]() ,故
,故
![]()
(2)設(shè)“易建聯(lián)在這兩場(chǎng)比賽中![]() 至少有一場(chǎng)超過(guò)
至少有一場(chǎng)超過(guò)![]() ”為事件
”為事件![]() ,則從上述
,則從上述![]() 場(chǎng)中隨機(jī)選擇兩場(chǎng)共有
場(chǎng)中隨機(jī)選擇兩場(chǎng)共有![]() 個(gè)基本事件,其中任意選擇兩場(chǎng)中,兩場(chǎng)中
個(gè)基本事件,其中任意選擇兩場(chǎng)中,兩場(chǎng)中![]() 都不超過(guò)
都不超過(guò)![]() 的共有
的共有![]() 個(gè)基本事件,故
個(gè)基本事件,故![]()
(3)不具有線性相關(guān)關(guān)系.
因?yàn)樯Ⅻc(diǎn)圖并不是分布在某一條直線的周?chē)@球是集體運(yùn)動(dòng),個(gè)人無(wú)法完全主宰一場(chǎng)比賽.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】某教師調(diào)查了![]() 名高三學(xué)生購(gòu)買(mǎi)的數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量,將統(tǒng)計(jì)數(shù)據(jù)制成如下表格:
名高三學(xué)生購(gòu)買(mǎi)的數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量,將統(tǒng)計(jì)數(shù)據(jù)制成如下表格:
男生 | 女生 | 總計(jì) | |
購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)超過(guò) |
|
|
|
購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)不超過(guò) |
|
|
|
總計(jì) |
|
|
|
(Ⅰ)根據(jù)表格中的數(shù)據(jù),是否有![]() 的把握認(rèn)為購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量與性別相關(guān);
的把握認(rèn)為購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)的數(shù)量與性別相關(guān);
(Ⅱ)從購(gòu)買(mǎi)數(shù)學(xué)課外輔導(dǎo)書(shū)不超過(guò)![]() 本的學(xué)生中,按照性別分層抽樣抽取
本的學(xué)生中,按照性別分層抽樣抽取![]() 人,再?gòu)倪@
人,再?gòu)倪@![]() 人中隨機(jī)抽取
人中隨機(jī)抽取![]() 人詢(xún)問(wèn)購(gòu)買(mǎi)原因,求恰有
人詢(xún)問(wèn)購(gòu)買(mǎi)原因,求恰有![]() 名男生被抽到的概率.
名男生被抽到的概率.
附:  ,
, ![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖是函數(shù) ![]() 的導(dǎo)函數(shù)
的導(dǎo)函數(shù) ![]() 的圖象,對(duì)此圖象,有如下結(jié)論:
的圖象,對(duì)此圖象,有如下結(jié)論:
①在區(qū)間(-2,1)內(nèi) ![]() 是增函數(shù);
是增函數(shù);
②在區(qū)間(1,3)內(nèi) ![]() 是減函數(shù);
是減函數(shù);
③在 ![]() 時(shí),
時(shí), ![]() 取得極大值;
取得極大值;
④在 ![]() 時(shí),
時(shí), ![]() 取得極小值。
取得極小值。
其中正確的是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖所示,一個(gè)圓柱形乒乓球筒,高為![]() 厘米,底面半徑為
厘米,底面半徑為![]() 厘米.球筒的上底和下底分別粘有一個(gè)乒乓球,乒乓球與球筒底面及側(cè)面均相切(球筒和乒乓球厚度忽略不計(jì)).一個(gè)平面與兩乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個(gè)橢圓,則該橢圓的離心率為( )
厘米.球筒的上底和下底分別粘有一個(gè)乒乓球,乒乓球與球筒底面及側(cè)面均相切(球筒和乒乓球厚度忽略不計(jì)).一個(gè)平面與兩乒乓球均相切,且此平面截球筒邊緣所得的圖形為一個(gè)橢圓,則該橢圓的離心率為( )
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在等腰直角三角形ABC中,AB=AC=4,點(diǎn)P是邊AB邊上異于AB的一點(diǎn),光線從點(diǎn)P出發(fā),經(jīng)BC,CA反射后又回到點(diǎn)P(如圖),若光線QR經(jīng)過(guò)△ABC的重心,則AP等于( )
A.2
B.1
C.![]()
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知p:﹣x2+2x﹣m<0對(duì)x∈R恒成立;q:x2+mx+1=0有兩個(gè)正根.若p∧q為假命題,p∨q為真命題,求m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,函數(shù)y=2sin(πx+φ),x∈R(其中0≤φ≤ ![]() )的圖象與y軸交于點(diǎn)(0,1).
)的圖象與y軸交于點(diǎn)(0,1). 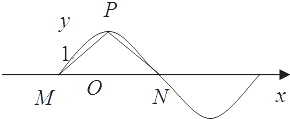
(1)求φ的值.
(2)設(shè)P是圖象上的最高點(diǎn),M、N是圖象與x軸的交點(diǎn),求tan∠MPN的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知{an}是等差數(shù)列,滿(mǎn)足a1=3,a4=12,數(shù)列{bn}滿(mǎn)足b1=4,b4=20,且{bn﹣an}為等比數(shù)列.
(1)求數(shù)列{an}和{bn}的通項(xiàng)公式;
(2)求數(shù)列{bn}的前n項(xiàng)和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】所謂正三棱錐,指的是底面為正三角形,頂點(diǎn)在底面上的射影為底面三角形中心的三棱錐,在正三棱錐S﹣ABC中,M是SC的中點(diǎn),且AM⊥SB,底面邊長(zhǎng)AB=2 ![]() ,則正三棱錐S﹣ABC的體積為 , 其外接球的表面積為 .
,則正三棱錐S﹣ABC的體積為 , 其外接球的表面積為 .
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com