
分析 根據正切函數的圖象及性質依次判斷即可.
解答 解:函數f(x)=tan(2x-$\frac{π}{4}$),
對于①:由題意,2x-$\frac{π}{4}$$≠\frac{π}{2}+kπ$,可得:x≠$\frac{1}{2}kπ+\frac{3π}{8}$.k∈Z.∴①對.
對于②:f(-x)=tan(-2x-$\frac{π}{4}$)=-tan(2x+$\frac{π}{4}$),f(-x)≠-f(x).∴函數f(x)不是奇函數,②不對.
對于③:令2x-$\frac{π}{4}$=$\frac{1}{2}$kπ,可得:x=$\frac{1}{4}kπ+\frac{π}{8}$,k為整數.當k=0時,可得圖象關于點($\frac{π}{8}$,0)對稱;∴③對.
對于④:令kπ$-\frac{π}{2}<2x-\frac{π}{4}<\frac{π}{2}$+kπ,可得:$\frac{1}{2}kπ-\frac{π}{8}<x<\frac{1}{2}kπ+\frac{3π}{8}$,∴④不對.
故答案為:①③.
點評 本題考查了正切函數的定義域,奇偶性,對稱性,單調性的運用.屬于基礎題.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
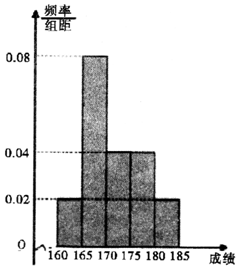 近期中央電視臺播出的《中國詩詞大會》火遍全國.某選拔賽后,隨機抽取100名選手的成績,按成績由低到高依次分為第1,2,3,4,5組,制成頻率分布直方圖如圖所示:
近期中央電視臺播出的《中國詩詞大會》火遍全國.某選拔賽后,隨機抽取100名選手的成績,按成績由低到高依次分為第1,2,3,4,5組,制成頻率分布直方圖如圖所示:查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 科學家利用魚的沉浮原理制造潛艇 | |
| B. | 猜想數列$\frac{1}{1×2}$,$\frac{1}{2×3}$,$\frac{1}{3×4}$,…的通項公式為an=$\frac{1}{n(n+1)}$(n∈N+) | |
| C. | 半徑為r的圓的面積S=πr2,則單位圓的面積S=π | |
| D. | 由平面直角坐標系中圓的方程為(x-a)2+(y-b)2=r2,推測空間直角坐標系中球的方程為(x-a)2+(y-b)2+(z-c)2=r2 |
查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | $y=sin(\frac{x}{2}+\frac{π}{3})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=cos(2x-\frac{π}{6})$ | D. | $y=tan(x+\frac{π}{6})$ |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com