【題目】已知函數
是定義在R上的偶函數，且當
時，
（
）.
（1）當
時，求的表達式：
（2）求在區間
的最大值
的表達式；
（3）當
時，若關于x的方程
（a，
）恰有10個不同實數解，求a的取值范圍.
【答案】（1）
；（2）
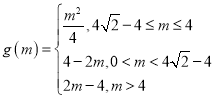；（3）
【解析】
（1）根據偶函數的特點，可知
，可得結果.
（2）采用分類討論方法，
與
，去掉絕對值研究函數
在區間
上的單調性，可得結果.
（3）畫出函數
圖像，利用換元法
，得出
與
，可轉化為
兩個根為
，可得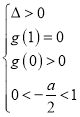
，最后計算可得結果.
（1）令
，則
由當
時，
所以
又函數是定義在R上的偶函數，
即
所以
所以當時，
（2）當時，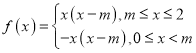
如圖
可知函數的最大值在
或
處取得，
所以
，
①若
，此時
②若
，此時
；
當時，
，對稱軸為
③若
，即
時，則，
④若
，即
時，則
綜上，得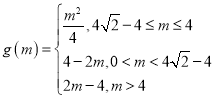
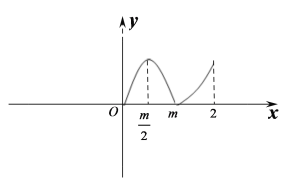
（3）當
時，
如圖
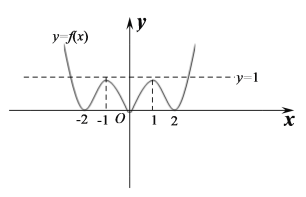
令
由的圖象可知，
當
時，方程
有兩解；
當
時，方程有四解；
當
時，方程有六解；
當
時，方程有三解；
當
時，方程無解.
要使方程
（a，
）
恰有10個不同實數解，
則關于t的方程
的一個根為1，
另一個根
，設，則有
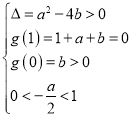
則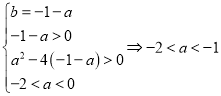
所以a的取值范圍為.
浙江新課程三維目標測評課時特訓系列答案
周周清檢測系列答案
輕巧奪冠周測月考直通高考系列答案科目：高中數學 來源： 題型：
【題目】下列說法錯誤的是（ ）
A.命題“若
，則
”的逆否命題是“若
，則
”
B.“
”是“
”的充分不必要條件
C.若
為假命題，則
、
均為假命題
D.命題：“
，使得
”，則非：“
，
”
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國是世界上嚴重缺水的國家，城市缺水問題較為突出，某市政府為了鼓勵居民節約用水，計劃在本市試行居民生活用水定額管理，即確定一個合理的居民月用水量標準：（單位：噸），用水量不超過
的部分按平價收費，超過的部分按議價收費，為了了解全布市民用用水量分布情況，通過袖樣，獲得了100位居民某年的月用水量（單位：噸），將數據按照
……
分成9組，制成了如圖所示的頻率分布直方圖
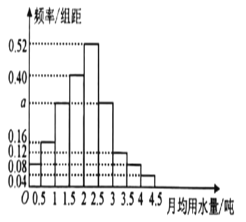
（1）求頻率分布直方圖中
的值；
（2）若該市政府看望使85%的居民每月的用水量不超過標準（噸），估計的值，并說明理由。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線
的極坐標方程是
,以極點為原點，以極軸為
軸的正半軸，取相同的單位長度，建立平面直角坐標系，直線
的參數方程為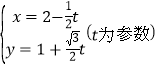
.
（1）寫出直線的普通方程與曲線的直角坐標方程；
（2）設曲線經過伸縮變換
得到曲線
，曲線上任一點為
，求
的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分13分）
為回饋顧客，某商場擬通過摸球兌獎的方式對1000位顧客進行獎勵，規定：每位顧客從一個裝有4個標有面值的球的袋中一次性隨機摸出2個球，球上所標的面值之和為該顧客所獲的獎勵額.
（1）若袋中所裝的4個球中有1個所標的面值為50元，其余3個均為10元，求
①顧客所獲的獎勵額為60元的概率
②顧客所獲的獎勵額的分布列及數學期望;
（2）商場對獎勵總額的預算是60000元，并規定袋中的4個球只能由標有面值10元和50元的兩種球組成，或標有面值20元和40元的兩種球組成.為了使顧客得到的獎勵總額盡可能符合商場的預算且每位顧客所獲的獎勵額相對均衡，請對袋中的4個球的面值給出一個合適的設計，并說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我校對高二600名學生進行了一次知識測試，并從中抽取了部分學生的成績（滿分100分）作為樣本，繪制了下面尚未完成的頻率分布表和頻率分布直方圖．
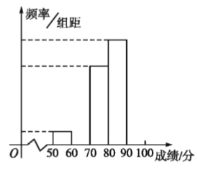
（1）填寫頻率分布表中的空格，補全頻率分布直方圖，并標出每個小矩形對應的縱軸數據；
分組 | 頻數 | 頻率 |
| 2 | 0．04 |
| 8 | 0．16 |
| 10 | ________ |
| ________ | ________ |
| 14 | 0．28 |
合計 | ________ | 1．00 |
（2）請你估算該年級學生成績的中位數；
（3）如果用分層抽樣的方法從樣本分數在
和
的人中共抽取6人，再從6人中選2人，求2人分數都在的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
