
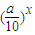 (0<a<10)的圖象上,且點Pn(an,bn)與點(n,0)和(n+1,0)構成一個以點Pn(an,bn)為頂點的等腰三角形.
(0<a<10)的圖象上,且點Pn(an,bn)與點(n,0)和(n+1,0)構成一個以點Pn(an,bn)為頂點的等腰三角形. ,再由點Pn(an,bn)在函數y=2000(
,再由點Pn(an,bn)在函數y=2000(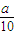 s)x(0<a<10)的圖象上查求出bn=2000
s)x(0<a<10)的圖象上查求出bn=2000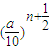 .
.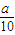 )2+(
)2+( )-1>0,由此可求出a的范圍.
)-1>0,由此可求出a的范圍.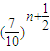 ≥1且2000
≥1且2000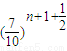 <1.從而{Bn}的最大項是第20項.
<1.從而{Bn}的最大項是第20項. ,又因為點Pn(an,bn)在函數y=2000(
,又因為點Pn(an,bn)在函數y=2000(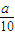 s)x(0<a<10)的圖象上,所以bn=2000
s)x(0<a<10)的圖象上,所以bn=2000 .
.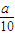 s)x(0<a<10)是單調遞減,所以對每一個自然數n有bn>bn+1>bn+2,
s)x(0<a<10)是單調遞減,所以對每一個自然數n有bn>bn+1>bn+2,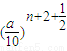 +2000
+2000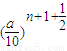 >2000
>2000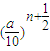 ,
,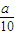 )2+(
)2+(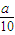 )-1>0,
)-1>0,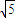 -1)<a<10.
-1)<a<10.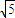 -1)<a<10且a是整數,所以a=7,因此bn=2000
-1)<a<10且a是整數,所以a=7,因此bn=2000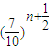 ,
,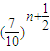 ≥1且2000
≥1且2000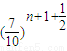 <1.
<1.

 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| a | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| a | 10 |
查看答案和解析>>
科目:高中數學 來源: 題型:
在xOy平面上有一點列P1(a1,b1),P2(a2,b2),…,Pn(an,bn)…,對每個自然數n點Pn位于函數y=2000(![]() )x(0<a<1)的圖像上,且點Pn,點(n,0)與點(n+1,0)構成一個以Pn為頂點的等腰三角形.
)x(0<a<1)的圖像上,且點Pn,點(n,0)與點(n+1,0)構成一個以Pn為頂點的等腰三角形.
(1)求點Pn的縱坐標bn的表達式;
(2)若對于每個自然數n,以bn,bn+1,bn+2為邊長能構成一個三角形,求a的取值范圍;
(3)設Cn=lg(bn)(n∈N*),若a取(2)中確定的范圍內的最小整數,問數列{Cn}前多少項的和最大?試說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
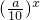 (0<a<10)的圖象上,且點Pn(an,bn)與點(n,0)和(n+1,0)構成一個以點Pn(an,bn)為頂點的等腰三角形.
(0<a<10)的圖象上,且點Pn(an,bn)與點(n,0)和(n+1,0)構成一個以點Pn(an,bn)為頂點的等腰三角形.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com