
【題目】已知正方形![]() 的邊長為2,分別以
的邊長為2,分別以![]() ,
, ![]() 為一邊在空間中作正三角形
為一邊在空間中作正三角形![]() ,
, ![]() ,延長
,延長![]() 到點
到點![]() ,使
,使![]() ,連接
,連接![]() ,
, ![]() .
.

(1)證明: ![]() 平面
平面![]() ;
;
(2)求點![]() 到平面
到平面![]() 的距離.
的距離.
【答案】(1)見解析;(2)1.
【解析】試題分析:(1)證線面垂直,先證線線垂直,做出輔助線,根據長度關系,首先證得![]() ,再證得
,再證得![]() ,
, ![]() ,根據線面垂直的判定定理得到線面垂直;(2)根據條件可得到
,根據線面垂直的判定定理得到線面垂直;(2)根據條件可得到![]() 平面
平面![]() ,進而點
,進而點![]() 到平面
到平面![]() 的距離等于
的距離等于![]() 點到平面
點到平面![]() 的距離,取
的距離,取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
, ![]() 平面
平面![]() ,
, ![]() 為點
為點![]() 到平面
到平面![]() 的距離.
的距離.
解析:
(1)連接![]() 交
交![]() 于點
于點![]() ,并連接
,并連接![]() ,則
,則![]() ,又∵
,又∵![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,∵
,∵![]() 平面
平面![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
即![]() ,∵
,∵![]() ,∴
,∴![]() 平面
平面![]() .
.
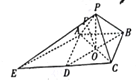
(2)由題知, ![]() ,且
,且![]() ,可得四邊形
,可得四邊形![]() 為平行四邊形,∴
為平行四邊形,∴![]() ,
,
又∵![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() ,∵點
,∵點![]() ,∴點
,∴點![]() 到平面
到平面![]() 的距離等于
的距離等于![]() 點到平面
點到平面![]() 的距離,取
的距離,取![]() 的中點為
的中點為![]() ,連接
,連接![]() ,則由(1)可得
,則由(1)可得![]() .
.
在![]() 中,
中, ![]() ,則
,則![]() ,∴
,∴![]() ,∴
,∴![]() 平面
平面![]() ,即
,即![]() 為點
為點![]() 到平面
到平面![]() 的距離.
的距離.
在![]() 中,
中, ![]() ,得點
,得點![]() 到平面
到平面![]() 的距離為1.
的距離為1.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:高中數學 來源: 題型:
【題目】某校高三課外興趣小組為了解高三同學高考結束后是否打算觀看2018年足球世界杯比賽的情況,從全校高三年級1500名男生、1000名女生中按分層抽樣的方式抽取125名學生進行問卷調查,情況如下表:
打算觀看 | 不打算觀看 | |
女生 | 20 | b |
男生 | c | 25 |
(1)求出表中數據b,c;
(2)判斷是否有99%的把握認為觀看2018年足球世界杯比賽與性別有關;
(3)為了計算“從10人中選出9人參加比賽”的情況有多少種,我們可以發現它與“從10人中選出1人不參加比賽”的情況有多少種是一致的.現有問題:在打算觀看2018年足球世界杯比賽的同學中有5名男生、2名女生來自高三(5)班,從中推選5人接受校園電視臺采訪,請根據上述方法,求被推選出的5人中恰有四名男生、一名女生的概率.
P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
K0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
附: 
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】深受廣大球迷喜愛的某支歐洲足球隊.在對球員的使用上總是進行數據分析,為了考察甲球員對球隊的貢獻,現作如下數據統計:
球隊勝 | 球隊負 | 總計 | |
甲參加 | 22 | b | 30 |
甲未參加 | c | 12 | d |
總計 | 30 | e | n |
(1)求b,c,d,e,n的值,據此能否有97.7%的把握認為球隊勝利與甲球員參賽有關;
(2)根據以往的數據統計,乙球員能夠勝任前鋒、中鋒、后衛以及守門員四個位置,且出場率分別為:0.2,0.5,0.2,0.1,當出任前鋒、中鋒、后衛以及守門員時,球隊輸球的概率依次為:0.4,0.2,0.6,0.2.則:
當他參加比賽時,求球隊某場比賽輸球的概率;
當他參加比賽時,在球隊輸了某場比賽的條件下,求乙球員擔當前鋒的概率;
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 7.879 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某印刷廠為了研究單冊書籍的成本![]() (單位:元)與印刷冊數
(單位:元)與印刷冊數![]() (單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
(單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:
印刷冊數 |
|
|
|
|
|
單冊成本 |
|
|
|
|
|
根據以上數據,技術人員分別借助甲、乙兩種不同的回歸模型,得到兩個回歸方程,方程甲:![]() ,方程乙:
,方程乙:![]() .
.
(1)為了評價兩種模型的擬合效果,完成以下任務.
①完成下表(計算結果精確到![]() );
);
印刷冊數 |
|
|
|
|
| |
單冊成本 |
|
|
|
|
| |
模型甲 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
模型乙 | 估計值 |
|
|
| ||
殘差 |
|
|
| |||
②分別計算模型甲與模型乙的殘差平方和,并通過比較,判斷哪個模型擬合效果更好.
(2)該書上市之后,受到廣大讀者熱烈歡迎,不久便全部售罄,于是印刷廠決定進行二次印刷,根據市場調查,新需求量為![]() 千冊,若印刷廠以每冊
千冊,若印刷廠以每冊![]() 元的價格將書籍出售給訂貨商,求印刷廠二次印刷
元的價格將書籍出售給訂貨商,求印刷廠二次印刷![]() 千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
千冊獲得的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】智能手機的出現,改變了我們的生活,同時也占用了我們大量的學習時間.某市教育機構從![]() 名手機使用者中隨機抽取
名手機使用者中隨機抽取![]() 名,得到每天使用手機時間(單位:分鐘)的頻率分布直方圖(如圖所示),其分組是:
名,得到每天使用手機時間(單位:分鐘)的頻率分布直方圖(如圖所示),其分組是: ![]() ,
,![]() .
.

(1)根據頻率分布直方圖,估計這![]() 名手機使用者中使用時間的中位數是多少分鐘? (精確到整數)
名手機使用者中使用時間的中位數是多少分鐘? (精確到整數)
(2)估計手機使用者平均每天使用手機多少分鐘? (同一組中的數據以這組數據所在區間中點的值作代表)
(3)在抽取的![]() 名手機使用者中在
名手機使用者中在![]() 和
和![]() 中按比例分別抽取
中按比例分別抽取![]() 人和
人和![]() 人組成研究小組,然后再從研究小組中選出
人組成研究小組,然后再從研究小組中選出![]() 名組長.求這
名組長.求這![]() 名組長分別選自
名組長分別選自![]() 和
和![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著互聯網的迅速發展,越來越多的消費者開始選擇網絡購物這種消費方式某營銷部門統計了2019年某月錦州的十大特產的網絡銷售情況得到網民對不同特產的最滿意度![]() 和對應的銷售額
和對應的銷售額![]() (萬元)數據,如下表:
(萬元)數據,如下表:
特產種類 | 甲 | 乙 | 丙 | 丁 | 戊 | 已 | 庚 | 辛 | 壬 | 癸 |
最滿意度 |
|
|
|
|
|
|
|
|
|
|
銷售額 |
|
|
|
|
|
|
|
|
|
|
![]() 求銷量額
求銷量額![]() 關于最滿意度
關于最滿意度![]() 的相關系數
的相關系數![]() ;
;
![]() 我們約定:銷量額
我們約定:銷量額![]() 關于最滿意度
關于最滿意度![]() 的相關系數
的相關系數![]() 的絕對值在
的絕對值在![]() 以上(含
以上(含![]() )是線性相關性較強;否則,線性相關性較弱.如果沒有達到較強線性相關,則采取“末位淘汰”制(即銷售額最少的特產退出銷售),并求在剔除“末位淘汰”的特產后的銷量額
)是線性相關性較強;否則,線性相關性較弱.如果沒有達到較強線性相關,則采取“末位淘汰”制(即銷售額最少的特產退出銷售),并求在剔除“末位淘汰”的特產后的銷量額![]() 關于最滿意度
關于最滿意度![]() 的線性回歸方程(系數精確到
的線性回歸方程(系數精確到![]() ).
).
參考數據:![]()
![]() ,
,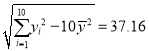 ,
,![]() ,
,![]() .
.
附:對于一組數據![]() .其回歸直線方程
.其回歸直線方程![]() 的斜率和截距的最小二乘法估計公式分別為:
的斜率和截距的最小二乘法估計公式分別為: ,
,![]() .線性相關系數
.線性相關系數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設an= ![]() sin
sin ![]() ,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正數的個數是( )
,Sn=a1+a2+…+an , 在S1 , S2 , …S100中,正數的個數是( )
A.25
B.50
C.75
D.100
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com