
【題目】如圖所示,現有一迷失方向的小青蛙在3處,它每跳動一次可以等可能地進入相鄰的任意一格(若它在5處,跳動一次,只能進入3處,若在3處,則跳動一次可以等機會進入1,2,4,5處),則它在第三次跳動后,首次進入5處的概率是( )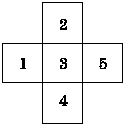
A.![]()
B.![]()
C.![]()
D.![]()
【答案】A
【解析】解:由題意可知小青蛙三次跳動后的所有情況有:
(3→1→3→1),(3→1→3→2),(3→1→3→4),(3→1→3→5);
(3→2→3→2),(3→2→3→1),(3→2→3→4),(3→2→3→5),
(3→4→3→4),(3→4→3→1),(3→4→3→2),(3→4→3→5),
(3→5→3→5),(3→5→3→1),(3→5→3→2),(3→5→3→4).
共有16種,
滿足題意的有:(3→1→3→5),(3→2→3→5),(3→4→3→5)有3種.
由古典概型的概率的計算公式可得:
青蛙在第三次跳動后,首次進入5處的概率是: ![]() .
.
故選:A.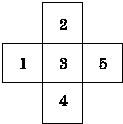
列出小青蛙三次跳動后的所有情況,找出滿足題意的可能數目,然后利用古典概型概率公式求解即可.


科目:高中數學 來源: 題型:
【題目】某保險公司針對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金.保險公司把企業的所有崗位共分為![]() 、
、![]() 、
、![]() 三類工種,從事三類工種的人數分布比例如圖,根據歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付頻率).
三類工種,從事三類工種的人數分布比例如圖,根據歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付頻率).
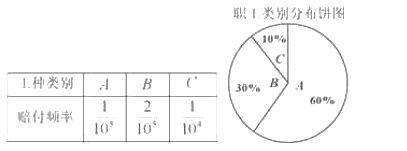
對于![]() 、
、![]() 、
、![]() 三類工種職工每人每年保費分別為
三類工種職工每人每年保費分別為![]() 元,
元,![]() 元,
元,![]() 元,出險后的賠償金額分別為100萬元,100萬元,50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
元,出險后的賠償金額分別為100萬元,100萬元,50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(Ⅰ)若保險公司要求利潤的期望不低于保費的20%,試確定保費![]() 、
、![]() 所要滿足的條件;
所要滿足的條件;
(Ⅱ)現有如下兩個方案供企業選擇;
方案1:企業不與保險公司合作,企業自行拿出與保險提供的等額的賠償金額賠付給出險職工;
方案2:企業于保險公司合作,企業負責職工保費的60%,職工個人負責保費的40%,出險后賠償金由保險公司賠付.
若企業選擇翻翻2的支出(不包括職工支出)低于選擇方案1的支出期望,求保費![]() 、
、![]() 所要滿足的條件,并判斷企業是否可與保險公司合作.(若企業選擇方案2的支出低于選擇方案1的支出期望,且與(Ⅰ)中保險公司所提條件不矛盾,則企業可與保險公司合作.)
所要滿足的條件,并判斷企業是否可與保險公司合作.(若企業選擇方案2的支出低于選擇方案1的支出期望,且與(Ⅰ)中保險公司所提條件不矛盾,則企業可與保險公司合作.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某市2017年3月1日至16日的空氣質量指數趨勢圖,空氣質量指數![]() 小于
小于![]() 表示空氣質量優良,空氣質量指數大于
表示空氣質量優良,空氣質量指數大于![]() 表示空氣重度污染,某人隨機選擇3月1日至3月14日中的某一天到達該市.
表示空氣重度污染,某人隨機選擇3月1日至3月14日中的某一天到達該市.
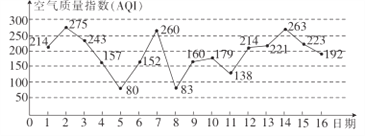
(1)若該人到達后停留![]() 天(到達當日算1天),求此人停留期間空氣質量都是重度污染的概率;
天(到達當日算1天),求此人停留期間空氣質量都是重度污染的概率;
(2)若該人到達后停留3天(到達當日算1天〉,設![]() 是此人停留期間空氣重度污染的天數,求
是此人停留期間空氣重度污染的天數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一個袋子內裝有2個綠球,3個黃球和若干個紅球(所有球除顏色外其他均相同),從中一次性任取2個球,每取得1個綠球得5分,每取得1個黃球得2分,每取得1個紅球得1分,用隨機變量![]() 表示2個球的總得分,已知得2分的概率為
表示2個球的總得分,已知得2分的概率為![]() .
.
(Ⅰ)求袋子內紅球的個數;
(Ⅱ)求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=aln(2x+1)+bx+1.
(1)若函數y=f(x)在x=1處取得極值,且曲線y=f(x)在點(0,f(0))處的切線與直線2x+y﹣3=0平行,求a的值;
(2)若 ![]() ,試討論函數y=f(x)的單調性.
,試討論函數y=f(x)的單調性.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知向量![]() ,
, ![]() ,且函數
,且函數![]() .
.
(Ⅰ)當函數![]() 在
在![]() 上的最大值為3時,求
上的最大值為3時,求![]() 的值;
的值;
(Ⅱ)在(Ⅰ)的條件下,若對任意的![]() ,函數
,函數![]() ,
, ![]() 的圖像與直線
的圖像與直線![]() 有且僅有兩個不同的交點,試確定
有且僅有兩個不同的交點,試確定![]() 的值.并求函數
的值.并求函數![]() 在
在![]() 上的單調遞減區間.
上的單調遞減區間.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某市的中學生中隨機調查了部分男生,獲得了他們的身高數據,整理得到如下頻率分布直方圖.
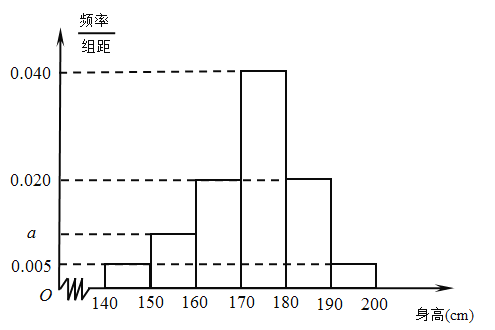
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)假設同組中的每個數據用該組區間的中點值代替,估計該市中學生中的全體男生的平均身高;
(Ⅲ)從該市的中學生中隨機抽取一名男生,根據直方圖中的信息,估計其身高在180 cm 以上的概率.若從全市中學的男生(人數眾多)中隨機抽取![]() 人,用
人,用![]() 表示身高在
表示身高在![]() 以上的男生人數,求隨機變量
以上的男生人數,求隨機變量![]() 的分布列和數學期望
的分布列和數學期望![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數y=f(x)是定義域為R的偶函數,當x≥0時,f(x)= 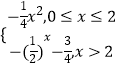 ,若關于x的方程[f(x)]2+af(x)+
,若關于x的方程[f(x)]2+af(x)+ ![]() =0,a∈R有且僅有8個不同實數根,則實數a的取值范圍是
=0,a∈R有且僅有8個不同實數根,則實數a的取值范圍是
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一家公司計劃生產某種小型產品的月固定成本為1萬元,每生產1萬件需要再投入2萬元,設該公司一個月內生產該小型產品x萬件并全部銷售完,每萬件的銷售收入為4﹣x萬元,且每萬件國家給予補助2e﹣ ![]() ﹣
﹣ ![]() 萬元.(e為自然對數的底數,e是一個常數)
萬元.(e為自然對數的底數,e是一個常數)
(1)寫出月利潤f(x)(萬元)關于月產量x(萬件)的函數解析式
(2)當月產量在[1,2e]萬件時,求該公司在生產這種小型產品中所獲得的月利潤最大值(萬元)及此時的月生成量值(萬件).(注:月利潤=月銷售收入+月國家補助﹣月總成本)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com