
在數列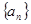 中,如果存在常數
中,如果存在常數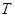
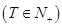 ,使得
,使得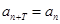 對于任意正整數
對于任意正整數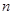 均成立,那么就稱數列
均成立,那么就稱數列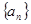 為周期數列,其中
為周期數列,其中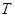 叫做數列
叫做數列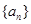 的周期. 已知數列
的周期. 已知數列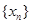 滿足
滿足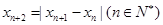 ,若
,若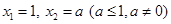 ,當數列
,當數列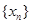 的周期為
的周期為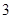 時,則數列
時,則數列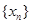 的前2012項的和
的前2012項的和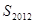 為( )
為( )
A.1339+a B.1340+a C.1341+a D.1342+a
D
【解析】
試題分析:先要弄清題意中所說的周期數列的含義,然后利用這個定義,針對題目中的數列的周期,先求x3,再前三項和s3,最后求s2012.
∵xn+1=|xn-xn-1|(n≥2,n∈N*),且x1=1,x2=a(a≤1,a≠0),∴x3=|x2-x1|=1-a,∴該數列的前3項的和s3=1+a+(1-a)=2∵數列{xn}周期為3,∴該數列的前2012項的和s2012=s2010+x1+x2=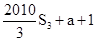 =1341+a,選B.
=1341+a,選B.
考點:本試題主要以周期數列為載體,考查數列具的周期性,考查該數列的前n項和.
點評:解決該試題的關鍵在于應由題意先求一個周期的和,再求該數列的前n項和sn.


科目:高中數學 來源: 題型:
| 1 | a-x |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5x-a | x+2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| kπ | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
(09年東城區二模理)(14分)
已知函數![]() =
=![]() (其中
(其中![]() 為常數,
為常數,![]() ).利用函數
).利用函數![]() 構造一個數列
構造一個數列![]() ,方法如下:
,方法如下:
對于給定的定義域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述構造過程中,如果![]() (
(![]() =1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果
=1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果![]() 不在定義域中,那么構造數列的過程就停止.
不在定義域中,那么構造數列的過程就停止.
(Ⅰ)當![]() 且
且![]() 時,求數列
時,求數列![]() 的通項公式;
的通項公式;
(Ⅱ)如果可以用上述方法構造出一個常數列,求![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:高中數學 來源: 題型:
(本小題滿分14分)
已知函數![]() 對于任意
對于任意![]() (
(![]() ),都有式子
),都有式子![]() 成立(其中
成立(其中![]() 為常數).
為常數).
(Ⅰ)求函數![]() 的解析式;
的解析式;
(Ⅱ)利用函數![]() 構造一個數列,方法如下:
構造一個數列,方法如下:
對于給定的定義域中的![]() ,令
,令![]() ,
,![]() ,…,
,…,![]() ,…
,…
在上述構造過程中,如果![]() (
(![]() =1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果
=1,2,3,…)在定義域中,那么構造數列的過程繼續下去;如果![]() 不在定義域中,那么構造數列的過程就停止.
不在定義域中,那么構造數列的過程就停止.
(ⅰ)如果可以用上述方法構造出一個常數列,求![]() 的取值范圍;
的取值范圍;
(ⅱ)是否存在一個實數![]() ,使得取定義域中的任一值作為
,使得取定義域中的任一值作為![]() ,都可用上述方法構造出一個無窮數列
,都可用上述方法構造出一個無窮數列![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由;
的值;若不存在,請說明理由;
(ⅲ)當![]() 時,若
時,若![]() ,求數列
,求數列![]() 的通項公式.
的通項公式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com