
 ,若對任意的正整數n,當m∈[-1,1]時,不等式
,若對任意的正整數n,當m∈[-1,1]時,不等式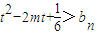 恒成立,求實數t的取值范圍.
恒成立,求實數t的取值范圍.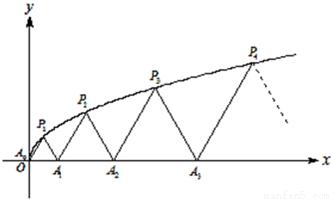
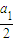 ,
,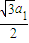 )代入到y2=3x中求出即可得到a1,然后同理求出a2和a3,然后猜想an=n(n+1)(n∈N*);
)代入到y2=3x中求出即可得到a1,然后同理求出a2和a3,然后猜想an=n(n+1)(n∈N*);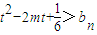 恒成立只需要求出bn的最大值,即可求出t的取值范圍.
恒成立只需要求出bn的最大值,即可求出t的取值范圍. ,
, )
) a12=
a12= a1,解得a1=2;
a1,解得a1=2;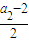 ,
,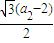 )代入到y2=3x中解得a2=6;
)代入到y2=3x中解得a2=6;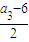 ,
, )代入到y2=3x中解得a3=12.
)代入到y2=3x中解得a3=12.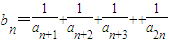

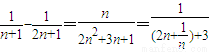 .
.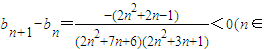 N*)
N*)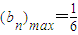 .
. (?n∈N*,?m∈[-1,1])
(?n∈N*,?m∈[-1,1])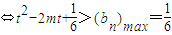 ,
,


 金鑰匙試卷系列答案
金鑰匙試卷系列答案科目:高中數學 來源: 題型:
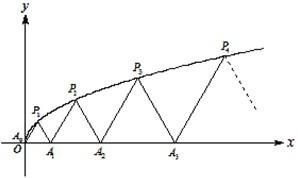 如圖,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…,n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).
如圖,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…,n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).查看答案和解析>>
科目:高中數學 來源: 題型:
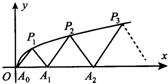 如圖,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…,n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).則a1=
如圖,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn)(0<y1<y2<…<yn)是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…,n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).則a1=查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…,n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).
如圖,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn)是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…,n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
| 1 |
| 6 |
查看答案和解析>>
科目:高中數學 來源: 題型:
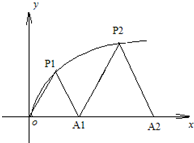 如圖,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).
如圖,P1(x1,y1)、P2(x2,y2)、…、Pn(xn,yn)(0<y1<y2<…<yn) 是曲線C:y2=3x(y≥0)上的n個點,點Ai(ai,0)(i=1,2,3,…n)在x軸的正半軸上,且△Ai-1AiPi是正三角形(A0是坐標原點).查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•閘北區二模)如圖,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲線C:y2=
(2012•閘北區二模)如圖,P1(x1,y1),P2(x2,y2),…,Pn(xn,yn),…是曲線C:y2=| 1 |
| 2 |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| an+3 |
| 1 |
| a2n |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com