
【題目】在直三棱柱![]() 中,
中,![]() 為正三角形,點
為正三角形,點![]() 在棱
在棱![]() 上,且
上,且![]() ,點
,點![]() 、
、![]() 分別為棱
分別為棱![]() 、
、![]() 的中點.
的中點.
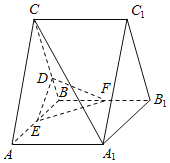
(1)證明:![]() 平面
平面![]() ;
;
(2)若![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)見解析;(2)![]() .
.
【解析】
(1)連接![]() ,連接
,連接![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,再連接
,再連接![]() ,證明出
,證明出![]() ,結合條件
,結合條件![]() 可得出
可得出![]() ,然后利用直線與平面平行的判定定理可證明出
,然后利用直線與平面平行的判定定理可證明出![]() 平面
平面![]() ;
;
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() ,證明出
,證明出![]() 平面
平面![]() ,且
,且![]() ,設等邊三角形
,設等邊三角形![]() 的邊長為
的邊長為![]() ,并設
,并設![]() ,以點
,以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,由
,由![]() 得出
得出![]() 的值,并計算出平面
的值,并計算出平面![]() 的法向量,利用空間向量法求出直線
的法向量,利用空間向量法求出直線![]() 與平面
與平面![]() 所成的角的正弦值.
所成的角的正弦值.
(1)如下圖所示,連接![]() ,連接
,連接![]() 分別交
分別交![]() 、
、![]() 于點
于點![]() 、
、![]() ,再連接
,再連接![]() ,
,
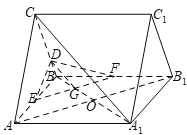
![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,則
的中點,則![]() ,
,![]() ,則
,則![]() 為
為![]() 的中點,
的中點,
在直三棱柱![]() 中,
中,![]() ,則四邊形
,則四邊形![]() 為平行四邊形,
為平行四邊形,
![]() ,
,![]() 為
為![]() 的中點,
的中點,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ;
;
(2)取![]() 的中點
的中點![]() ,連接
,連接![]() 、
、![]() ,
,
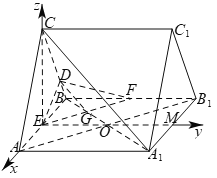
![]() 四邊形
四邊形![]() 為平行四邊形,則
為平行四邊形,則![]() ,
,
![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點,
的中點,![]() ,所以,四邊形
,所以,四邊形![]() 是平行四邊形,
是平行四邊形,
![]() ,在直三棱柱
,在直三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 是等邊三角形,且點
是等邊三角形,且點![]() 是
是![]() 的中點,
的中點,![]() ,
,
以點![]() 為坐標原點,
為坐標原點,![]() 、
、![]() 、
、![]() 所在直線分別為
所在直線分別為![]() 軸、
軸、![]() 軸、
軸、![]() 軸建立空間直角坐標系
軸建立空間直角坐標系![]() ,
,
設![]() 的邊長為
的邊長為![]() ,
,![]() ,則點
,則點![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、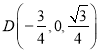 、
、![]() ,
,![]() ,
,![]() ,
,
![]() ,則
,則![]() ,得
,得![]() ,
,
![]() ,
,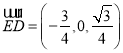 ,
,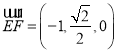 .
.
設平面![]() 的法向量為
的法向量為![]() ,由
,由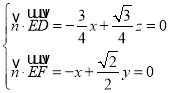 ,得
,得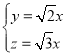 .
.
令![]() ,可得
,可得![]() ,
,![]() ,所以,平面
,所以,平面![]() 的一個法向量為
的一個法向量為![]() ,
,
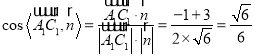 ,
,
因此,直線![]() 與平面
與平面![]() 所成的角的正弦值為
所成的角的正弦值為![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】(本小題滿分12分)如圖,三棱柱ABC-A1B1C1中,CA=CB,AB=A A1,∠BA A1=60°.
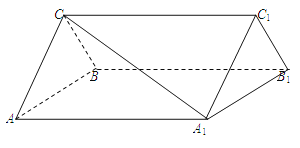
(Ⅰ)證明AB⊥A1C;
(Ⅱ)若平面ABC⊥平面AA1B1B,AB=CB,求直線A1C 與平面BB1C1C所成角的正弦值。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
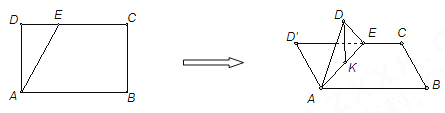
【題目】如圖,在長方形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 為線段
為線段![]() 上一動點,現(xiàn)將
上一動點,現(xiàn)將![]() 沿
沿![]() 折起,使點
折起,使點![]() 在面
在面![]() 內的射影
內的射影![]() 在直線
在直線![]() 上,當點
上,當點![]() 從
從![]() 運動到
運動到![]() ,則點
,則點![]() 所形成軌跡的長度為( )
所形成軌跡的長度為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】命題![]() 方程
方程![]() 表示雙曲線;命題
表示雙曲線;命題![]() 不等式
不等式![]() 的解集是
的解集是![]() .
. ![]() 為假,
為假, ![]() 為真,求
為真,求![]() 的取值范圍.
的取值范圍.
【答案】![]()
【解析】試題分析:由命題![]() 方程
方程![]() 表示雙曲線,求出
表示雙曲線,求出![]() 的取值范圍,由命題
的取值范圍,由命題![]() 不等式
不等式![]() 的解集是
的解集是![]() ,求出
,求出![]() 的取值范圍,由
的取值范圍,由![]() 為假,
為假, ![]() 為真,得出
為真,得出![]() 一真一假,分兩種情況即可得出
一真一假,分兩種情況即可得出![]() 的取值范圍.
的取值范圍.
試題解析:
![]() 真
真 ![]()
![]() ,
,
![]() 真
真 ![]() 或
或![]()
![]()
∴![]()
![]() 真
真![]() 假
假 ![]()
![]() 假
假![]() 真
真 ![]()
∴![]() 范圍為
范圍為![]()
【題型】解答題
【結束】
18
【題目】如圖,設![]() 是圓
是圓![]() 上的動點,點
上的動點,點![]() 是
是![]() 在
在![]() 軸上的投影,
軸上的投影, ![]() 為
為![]() 上一點,且
上一點,且![]() .
.

(1)當![]() 在圓上運動時,求點
在圓上運動時,求點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)求過點![]() 且斜率為
且斜率為![]() 的直線被
的直線被![]() 所截線段的長度.
所截線段的長度.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某工廠的機器上有一種易損元件A,這種元件在使用過程中發(fā)生損壞時,需要送維修處維修.工廠規(guī)定當日損壞的元件A在次日早上 8:30 之前送到維修處,并要求維修人員當日必須完成所有損壞元件A的維修工作.每個工人獨立維修A元件需要時間相同.維修處記錄了某月從1日到20日每天維修元件A的個數(shù),具體數(shù)據(jù)如下表:
日期 | 1 日 | 2 日 | 3 日 | 4 日 | 5 日 | 6 日 | 7 日 | 8 日 | 9 日 | 10 日 |
元件A個數(shù) | 9 | 15 | 12 | 18 | 12 | 18 | 9 | 9 | 24 | 12 |
日期 | 11 日 | 12 日 | 13 日 | 14 日 | 15 日 | 16 日 | 17 日 | 18 日 | 19 日 | 20 日 |
元件A個數(shù) | 12 | 24 | 15 | 15 | 15 | 12 | 15 | 15 | 15 | 24 |
從這20天中隨機選取一天,隨機變量X表示在維修處該天元件A的維修個數(shù).
(Ⅰ)求X的分布列與數(shù)學期望;
(Ⅱ)若a,b![]() ,且b-a=6,求
,且b-a=6,求![]() 最大值;
最大值;
(Ⅲ)目前維修處有兩名工人從事維修工作,為使每個維修工人每天維修元件A的個數(shù)的數(shù)學期望不超過4個,至少需要增加幾名維修工人?(只需寫出結論)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】(多選)已知函數(shù)![]() ,其中正確結論的是( )
,其中正確結論的是( )
A.當![]() 時,函數(shù)
時,函數(shù)![]() 有最大值.
有最大值.
B.對于任意的![]() ,函數(shù)
,函數(shù)![]() 一定存在最小值.
一定存在最小值.
C.對于任意的![]() ,函數(shù)
,函數(shù)![]() 是
是![]() 上的增函數(shù).
上的增函數(shù).
D.對于任意的![]() ,都有函數(shù)
,都有函數(shù)![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知點
中,已知點![]() ,圓
,圓![]() :
:![]() 與
與![]() 軸的正半軸的交點是
軸的正半軸的交點是![]() ,過點
,過點![]() 的直線
的直線![]() 與圓
與圓![]() 交于不同的兩點
交于不同的兩點![]() .
.

(1)若直線![]() 與
與![]() 軸交于
軸交于![]() ,且
,且![]() ,求直線
,求直線![]() 的方程;
的方程;
(2)設直線![]() ,
,![]() 的斜率分別是
的斜率分別是![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)設![]() 的中點為
的中點為![]() ,點
,點![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com