
【題目】已知函數![]() ,其中
,其中![]() ,給出四個結論:
,給出四個結論:
①函數![]() 是最小正周期為
是最小正周期為![]() 的奇函數;
的奇函數;
②函數![]() 的圖像的一條對稱軸是
的圖像的一條對稱軸是![]() ;
;
③函數![]() 圖像的一個對稱中心是
圖像的一個對稱中心是![]() ;
;
④函數![]() 的遞增區間為
的遞增區間為![]() .則正確結論的個數為( )
.則正確結論的個數為( )
A. 4個 B. 3個 C. 2個 D. 1個
【答案】B
【解析】解答:
∵![]()
=cos2xcos![]() sin2xsin
sin2xsin![]() cos2x=
cos2x=![]() cos2x
cos2x![]() sin2xcos2x=
sin2xcos2x=![]() sin2x
sin2x![]() cos2x=sin(2x+
cos2x=sin(2x+![]() )
)
∴T=π,即函數f(x)的最小正周期為π,
但f(0)=sin![]() =
=![]() ≠0,函數f(x)不是奇函數。命題①錯誤;
≠0,函數f(x)不是奇函數。命題①錯誤;
∵f(![]() )=sin(2×
)=sin(2×![]() +
+![]() )=sin
)=sin![]() =1,
=1,
∴函數f(x)圖象的一條對稱軸是x=![]() .命題②正確;
.命題②正確;
∵f(![]() )=sin(2×
)=sin(2×![]() +
+![]() )=sinπ=0,
)=sinπ=0,
∴函數f(x)圖象的一個對稱中心為(![]() ,0).命題③正確;
,0).命題③正確;
由![]() +2kπ2x+
+2kπ2x+![]()
![]() +2kπ,得:
+2kπ,得:
![]() +kπx
+kπx![]() +kπ,k∈Z.
+kπ,k∈Z.
∴函數f(x)的遞增區間為[kπ+![]() ,kπ+
,kπ+![]() ],k∈Z.命題④正確。
],k∈Z.命題④正確。
∴正確結論的個數是3個。
故選:B.


 每課必練系列答案
每課必練系列答案科目:高中數學 來源: 題型:
【題目】某知名品牌汽車深受消費者喜愛,但價格昂貴。某汽車經銷商推出![]() 三種分期付款方式銷售該品牌汽車,并對近期100位采用上述分期付款的客戶進行統計分析,得到如下的柱狀圖。已知從
三種分期付款方式銷售該品牌汽車,并對近期100位采用上述分期付款的客戶進行統計分析,得到如下的柱狀圖。已知從![]() 三種分期付款銷售中,該經銷商每銷售此品牌汽車1輛所獲得的利潤分別是1萬元,2萬元,3萬元。以這100 位客戶所采用的分期付款方式的頻率代替1位客戶采用相應分期付款方式的概率。
三種分期付款銷售中,該經銷商每銷售此品牌汽車1輛所獲得的利潤分別是1萬元,2萬元,3萬元。以這100 位客戶所采用的分期付款方式的頻率代替1位客戶采用相應分期付款方式的概率。

(Ⅰ)求采用上述分期付款方式銷售此品牌汽車1輛,該汽車經銷商從中所獲得的利潤不大于2萬元的概率;
(Ⅱ)求采用上述分期付款方式銷售此品牌汽車1輛,該汽車經銷商從中所獲得的利潤的平均值;
(Ⅲ)根據某稅收規定,該汽車經銷商每月(按30天計)上交稅收的標準如下表:
![]()
若該經銷商按上述分期付款方式每天平均銷售此品牌汽車3輛,估計其月純收入(純收入=總利潤-上交稅款)的平均值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查喜歡旅游是否與性別有關,調查人員就“是否喜歡旅游”這個問題,在火車站分別隨機調研了![]() 名女性或
名女性或![]() 名男性,根據調研結果得到如圖所示的等高條形圖.
名男性,根據調研結果得到如圖所示的等高條形圖.
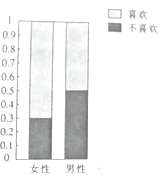
(1)完成下列 ![]() 列聯表:
列聯表:
喜歡旅游 | 不喜歡旅游 | 估計 | |
女性 | |||
男性 | |||
合計 |
(2)能否在犯錯誤概率不超過![]() 的前提下認為“喜歡旅游與性別有關”.
的前提下認為“喜歡旅游與性別有關”.
附:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式:
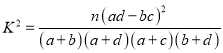 ,其中
,其中![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某高中在校學生2 000人,高一年級與高二年級人數相同并且都比高三年級多1人.為了響應市教育局“陽光體育”號召,該校開展了跑步和跳繩兩項比賽,要求每人都參加而且只參加其中一項,各年級參與項目人數情況如下表:
年級 項目 | 高一年級 | 高二年級 | 高三年級 |
跑步 | a | b | c |
跳繩 | x | y | z |
其中a∶b∶c=2∶3∶5,全校參與跳繩的人數占總人數的![]() . 為了了解學生對本次活動的滿意度,采用分層抽樣從中抽取一個200人的樣本進行調查,則高二年級中參與跑步的同學應抽取多少人?
. 為了了解學生對本次活動的滿意度,采用分層抽樣從中抽取一個200人的樣本進行調查,則高二年級中參與跑步的同學應抽取多少人?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2017年“一帶一路”國際合作高峰論壇于今年5月14日至15日在北京舉行.為高標準完成高峰論壇會議期間的志愿服務工作,將從27所北京高校招募大學生志愿者,某調查機構從是否有意愿做志愿者在某高校訪問了80人,經過統計,得到如下丟失數據的列聯表:(![]() ,表示丟失的數據)
,表示丟失的數據)
無意愿 | 有意愿 | 總計 | |
男 |
|
| 40 |
女 | 5 |
|
|
總計 | 25 |
| 80 |
(1)求出![]() 的值,并判斷:能否有99.9%的把握認為有意愿做志愿者與性別有關;
的值,并判斷:能否有99.9%的把握認為有意愿做志愿者與性別有關;
(2)若表中無意愿做志愿者的5個女同學中,3個是大學三年級同學,2個是大學四年級同學.現從這5個同學中隨機選2同學進行進一步調查,求這2個同學是同年級的概率.
附參考公式及數據: 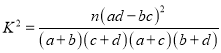 ,其中
,其中![]() .
.
| 0.40 | 0.25 | 0.10 | 0.010 | 0.005 | 0.001 |
| 0.708 | 1.323 | 2.706 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),在以原點為極點,
為參數),在以原點為極點, ![]() 軸正半軸為極軸的極坐標系中,直線
軸正半軸為極軸的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的傾斜角;
的傾斜角;
(2)設點![]() ,
, ![]() 和
和![]() 交于
交于![]() 兩點,求
兩點,求![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,已知四棱錐![]() 的底面為矩形,D為
的底面為矩形,D為![]() 的中點,AC⊥平面BCC1B1.
的中點,AC⊥平面BCC1B1.

(Ⅰ)證明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的長;
(2)求B1D與平面ABB1所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的極坐標方程是
的極坐標方程是![]() ,以極點為原點,極軸為
,以極點為原點,極軸為![]() 軸的正半軸建立平面直角坐標系,直線
軸的正半軸建立平面直角坐標系,直線![]() 的參數方程為
的參數方程為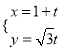 (
(![]() 為參數).
為參數).
(Ⅰ)寫出直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(Ⅱ)設曲線![]() 經過伸縮變換
經過伸縮變換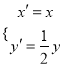 得到曲線
得到曲線![]() ,若點
,若點![]() ,直線
,直線![]() 與
與![]() 交與
交與![]() ,
, ![]() ,求
,求![]() ,
, ![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com