
(2007
遼寧,21)已知數列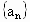 、
、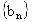 與函數f(x)、g(x),x
與函數f(x)、g(x),x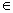 R滿足條件:
R滿足條件: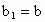 ,
,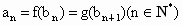 .
.
(1)
若f(x)=tx+1(t≠0,t≠2),g(x)=2x,f(b)≠g(b),且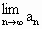 存在,求t的取值范圍,并求
存在,求t的取值范圍,并求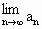 (用t表示);
(用t表示);
(2)
若函數y=f(x)為R上的增函數,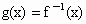 ,b=1,f(1)<1,證明對任意的
,b=1,f(1)<1,證明對任意的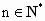 ,
,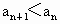 .
. |
解析: (1)解法一:由題設知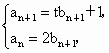 得 得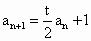 .又已知t≠2,可得 .又已知t≠2,可得 . .
由 f(b)≠g(b),t≠2,t≠0,可知 , ,
所以 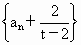 是等比數列,其首項為 是等比數列,其首項為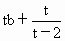 , ,
公比為 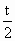 .于是 .于是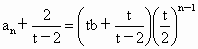 , ,
即 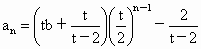 .又 .又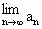 存在,可得 存在,可得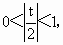
所以- 2<t<2且t≠0.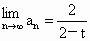 . .
解法二:由題設知 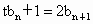 , ,
且 t≠2,可得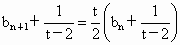 . .
由 f(b)≠g(b),t≠2,t≠0,可知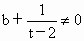 , ,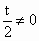 ,所以 ,所以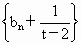 是首項為 是首項為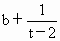 ,公比為 ,公比為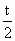 的等比數列. 的等比數列.
即 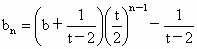 . .
由 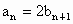 可知,若 可知,若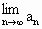 存在,則 存在,則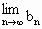 存在. 存在.
于是可得 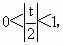 所以-2<t<2且t≠0. 所以-2<t<2且t≠0.
解法三:由題設知 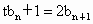 ,即 ,即
②-①得 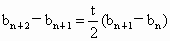 , ,
令 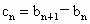 ,得 ,得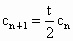 . .
由 f(b)≠g(b),t≠2,t≠0可得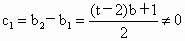 , ,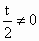 ,所以 ,所以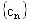 是首項為 是首項為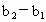 ,公比為 ,公比為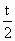 的等比數列. 的等比數列.
于是 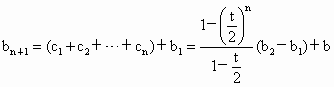 , ,
又 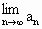 存在,可得 存在,可得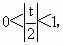
所以- 2<t<2且t≠0.
說明:數列 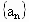 通項公式的求法和結果的表達形式均不唯一,其他過程和結果參照以上評分標準. 通項公式的求法和結果的表達形式均不唯一,其他過程和結果參照以上評分標準.
(2) 證明:因為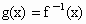 , ,
所以 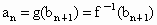 ,即 ,即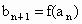 . .
下面用數學歸納法證明 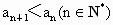 . .
①當 n=1時,由f(x)為增函數,且 f(1)<1,得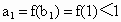 , ,
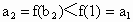 , ,
即 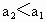 ,結論成立. ,結論成立.
②假設 n=k時結論成立,即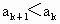 . .
由 f(x)為增函數,得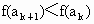 ,即 ,即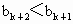 , ,
進而得 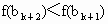 ,即 ,即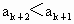 . .
這就是說當 n=k+1時,結論也成立.根據①和②可知,對任意的  , ,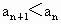 . . |
|
剖析:本題主要考查數列的定義、數列的遞推公式、等比數列、函數、不等式等基礎知識,考查運用數學歸納法解決問題的能力. |


湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com