解:(1)∵
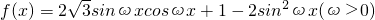
∴利用三角函數的降次公式,得f(x)=

sin(2ωx)+cos(2ωx)=2sin(2ωx+

)
∵函數f(x)的最小正周期為T=

=π
∴2ω=2,可得函數f(x)的解析式為:y=2sin(2x+

)
令

<2x+

<
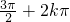
,得

+kπ<x<

+kπ,其中k是整數,
∵
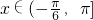
,
∴取k=0,得x∈
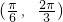
所以函數f(x)的單調遞減區間是
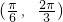
;
(2)函數y=f(x)的圖象上各點的縱坐標保持不變,橫坐標縮短到原來的

,
所得函數解析式為:y=2sin(4x+

)
再把所得到的圖象再向左平移

個單位,得到函數y=g(x)的圖象,
∴g(x)=2sin[4(x+

)+

]=2sin(4x+

)
∵函數y=g(x)定義在區間
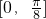
上,
∴4x+

∈[

,

]?sin

≤sin(4x+

)≤sin

即-

≤sin(4x+

)≤

∴函數y=g(x)的值域為[-

,1],函數的最小值為-

.
分析:(1)利用三角函數的降次公式進行化簡,得f(x)=2sin(2ωx+

),根據函數y=Asin(ωx+φ)的周期的公式,計算出ω的值,得到函數的表達式,最后根據函數函數y=Asin(ωx+φ)的單調區間的結論,可以求得函數f(x)的單調遞減區間;
(2)根據函數y=Asin(ωx+φ)的圖象變換的規律,得到變換后函數y=g(x)的解析式是:g(x)=2sin(4x+

),然后根據函數y=Asin(ωx+φ)的單調性的結論,可得函數g(x)在區間
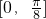
上的值域,從而得到y=g(x)在區間
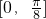
上的最小值.
點評:本題以一個特殊的三角函數為例加以研究,著重考查了三角函數中的恒等變換、函數y=Asin(ωx+φ)的圖象和性質和三角函數的最值等知識點,屬于中檔題.

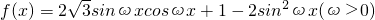 ,且函數f(x)的最小正周期為π.
,且函數f(x)的最小正周期為π.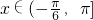 ,求函數f(x)的單調遞減區間;
,求函數f(x)的單調遞減區間; ,把所得到的圖象再向左平移
,把所得到的圖象再向左平移 個單位,得到函數y=g(x)的圖象,求函數y=g(x)在區間
個單位,得到函數y=g(x)的圖象,求函數y=g(x)在區間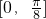 上的最小值.
上的最小值.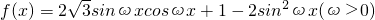
 sin(2ωx)+cos(2ωx)=2sin(2ωx+
sin(2ωx)+cos(2ωx)=2sin(2ωx+ )
) =π
=π )
) <2x+
<2x+ <
<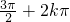 ,得
,得 +kπ<x<
+kπ<x< +kπ,其中k是整數,
+kπ,其中k是整數,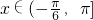 ,
,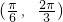
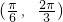 ;
; ,
, )
) 個單位,得到函數y=g(x)的圖象,
個單位,得到函數y=g(x)的圖象, )+
)+ ]=2sin(4x+
]=2sin(4x+ )
)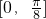 上,
上, ∈[
∈[ ,
, ]?sin
]?sin ≤sin(4x+
≤sin(4x+ )≤sin
)≤sin
 ≤sin(4x+
≤sin(4x+ )≤
)≤
 ,1],函數的最小值為-
,1],函數的最小值為- .
. ),根據函數y=Asin(ωx+φ)的周期的公式,計算出ω的值,得到函數的表達式,最后根據函數函數y=Asin(ωx+φ)的單調區間的結論,可以求得函數f(x)的單調遞減區間;
),根據函數y=Asin(ωx+φ)的周期的公式,計算出ω的值,得到函數的表達式,最后根據函數函數y=Asin(ωx+φ)的單調區間的結論,可以求得函數f(x)的單調遞減區間; ),然后根據函數y=Asin(ωx+φ)的單調性的結論,可得函數g(x)在區間
),然后根據函數y=Asin(ωx+φ)的單調性的結論,可得函數g(x)在區間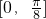 上的值域,從而得到y=g(x)在區間
上的值域,從而得到y=g(x)在區間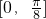 上的最小值.
上的最小值.
