
【題目】矩形![]() 的兩條對角線相交于點
的兩條對角線相交于點![]() ,
, ![]() 邊所在直線的方程為
邊所在直線的方程為![]() ,點
,點![]() 在
在![]() 邊所在直線上.
邊所在直線上.
(Ⅰ)求![]() 邊所在直線的方程;
邊所在直線的方程;
(Ⅱ)求矩形![]() 外接圓的方程;
外接圓的方程;
【答案】(1) ![]() (2)
(2) ![]()
【解析】試題分析:(I)由已知中AB邊所在直線的方程![]() ,且AD與AB垂直,我們可以求出直線AD的斜率,結合點
,且AD與AB垂直,我們可以求出直線AD的斜率,結合點![]() 在直線AD上,可得到AD邊所在直線的點斜式方程,進而再化為一般式方程.
在直線AD上,可得到AD邊所在直線的點斜式方程,進而再化為一般式方程.
(II)根據矩形的性質可得矩形ABCD外接圓圓心即為兩條對角線交點M(2,0),根據(I)中直線AB,AD的直線方程求出A點坐標,進而根據AM長即為圓的半徑,得到矩形ABCD外接圓的方程.
試題解析:
(I)因為![]() 邊所在直線的方程為
邊所在直線的方程為![]() ,且
,且![]() 與
與![]() 垂直,所以直線
垂直,所以直線![]() 的斜率為
的斜率為![]() .又因為點
.又因為點![]() 在直線
在直線![]() 上,
上,
所以![]() 邊所在直線的方程為
邊所在直線的方程為![]() .即
.即![]() .
.
(II)由![]() 解得點
解得點![]() 的坐標為
的坐標為![]() ,
,
因為矩形![]() 兩條對角線的交點為
兩條對角線的交點為![]() .所以
.所以![]() 為矩形外接圓的圓心.
為矩形外接圓的圓心.
又![]() .
.
從而矩形![]() 外接圓的方程為
外接圓的方程為![]() .
.


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:高中數學 來源: 題型:
【題目】如圖,AB是圓O的直徑,PA垂直圓所在的平面,C是圓上的點.
(1)求證:平面PAC⊥平面PBC;
(2)若AC=1,PA=1,求圓心O到平面PBC的距離.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=1,AD=2,E是AD的中點,O是AC與BE的交點,將△ABE沿BE折起到△A1BE的位置,如圖2.
,AB=BC=1,AD=2,E是AD的中點,O是AC與BE的交點,將△ABE沿BE折起到△A1BE的位置,如圖2.
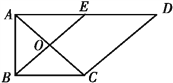
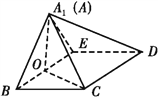
圖1 圖2
(1)證明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC與平面A1CD夾角的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知m>0, ![]() ,
, ![]() .
.
(1) 若p是q的充分不必要條件,求實數m的取值范圍;
(2) 若m=5,“![]() ”為真命題,“
”為真命題,“![]() ”為假命題,求實數x的取值范圍.
”為假命題,求實數x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com