
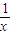 .
.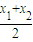 )與
)與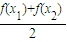 的大小.
的大小.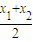 )-
)-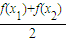 化簡整理后判定其符號.
化簡整理后判定其符號.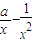
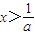 ,
,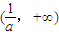 ;
;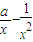 <0,解得
<0,解得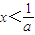 ,
,
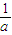 時,函數f(x)有極小值,
時,函數f(x)有極小值,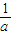 )=
)=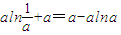
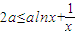 恒成立,
恒成立,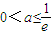
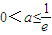
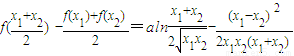
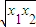 ,∴
,∴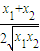 >1,aln
>1,aln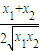 <0
<0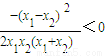 ,
,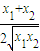 +
+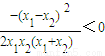 ,
,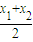 )-
)-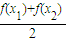 <0,即f(
<0,即f(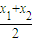 )<
)<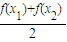 .
.

科目:高中數學 來源: 題型:
| a-x2 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com