Question

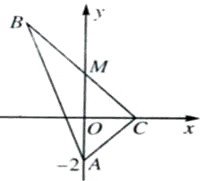
如圖所示，在△ABC中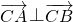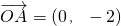，，，M在y軸上，且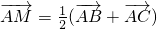，C在x軸上移動．
（Ⅰ）求點B的軌跡E的方程；
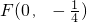（Ⅱ）過點的直線l交軌跡E于H，G兩點（H在F，G之間），若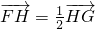，求直線l的斜率．

Answer 1

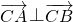解：（Ⅰ）設B（x，y），C（a，0），M（0，b），a≠0，∵，即∠ACB=90°∴，
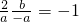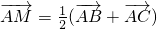于是a²=2b①M在y軸上，且，∴M是BC的中點，可得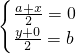∴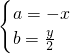②
把②代入①得y=x²（x≠0），所以B的軌跡E的方程為y=x²（x≠0）（6分）
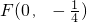（Ⅱ）點，設滿足條件的直線l的方程為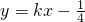，H（x₁，y₁），G（x₂，y₂）
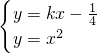由得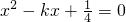，△=k²-1＞0，∴k²＞1，
∵，
∴，
∴，
∴3x₁=x₂，
∵x₁+x₂=k，，
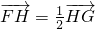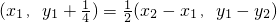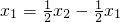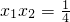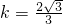∴（13分）
直線l的斜率：．
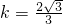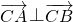分析：（Ⅰ）先設B（x，y），C（a，0），M（0，b），a≠0，根據，得出∠ACB=90°，于是a²=2b，再結合M在y軸上，及題中向量關系得出M是BC的中點，x，y的關系式即為B的軌跡E的方程；
（Ⅱ）設滿足條件的直線l的方程，將直線的方程代入拋物線的方程，消去y得到關于x的一元二次方程，再結合根系數的關系利用向量關系式即可求得k值，從而解決問題．
點評：本題考查直線和圓錐曲線的位置關系，解題時要認真審題，提高解題能力和解題時技巧，注意合理地進行等價轉化．